You can find the source code at Google Code for this project in the iPhone Bits repository. You can check out a copy of the project by typing the following command in a terminal window:
svn checkout http://iphonebits.googlecode.com/svn/trunk/src/PirateFlag PirateFlag
Note: If you have problems getting it to run, trying using Debug instead of Run. I'm trying to figure out what's causing that now.
Actually, this isn't exactly a port of NeHe #11, it's more of a re-implementation. This is a common tutorial that's been done many times in many places including on NeHe and at ZeusCMD. Similar tutorials are also featured in some books like OpenGL Game Programming.
There's a video of this code in action right here.
This isn't a real physics simulation. All we do is create a grid of vertices and move the z-coordinate along a sine wave. It does look a little like a flag blowing in the breeze, though, and it's certainly less computationally expensive than a real physics simulation would be, especially the way we're going to do it here. There are two basic approaches that fake-flag tutorials usually take. One is to calculate the location along the sine wave every time you go to draw. This is a more accurate method in that you can be very precise and take the exact amount of time elapsed since the previous frame was drawn into account. The second way is less accurate but uses far less processing power. The second approach is to pre-calculate the position for every spot on a grid and use those grids as vertices. Then each frame, you assign each vertex its neighbors value, taking the position of the last column of vertices and assigning it to the first column. That way, you get a continuous sine way but only have to calculate the positions once. This method is imprecise, but fine for many purposes (say, for a flag on a flagpole used as a background element in a game).
The grid of vertices that will represent our flag is just a two-dimensional array of Vertex3D structs. Remember, Vertex3D is just a structs with three GLfloat members representing the three cartesian coordinates of the point (x, y, z). Here's how we declare the grid:
Vertex3D flagVertices;And here's how we pre-calculate the initial values:
for (int x = 0; x < FLAG_X_POINTS; x++)
FLAG_X_POINTS and FLAG_Y_POINTS are pre-compiler macros that define the height and width of our grid. The project is currently set to a 36x20 grid, though you can play with those values if you want.
The yPoints variable is a fudge to make the sine wave loop nicely. I plan to revisit it at some point and fix the algorithm so it's not necessary, but sometimes you can get a result faster by trial end error, and that's what happened here. I kept adding one to the value used as the divisor until I got an even loop. Inelegant, but functional. If anyone feels like challenging themselves, please feel free to fix the algorithm so the fudge is not necessary. I do not ever mind having my code corrected.
Because we're going to map a texture to our flag, we need to use smooth shading (GL_SMOOTH), and we're going to add some lights to make things look a little more realistic. Once we get lights in the mix in OpenGL, then we need to calculate normals, and since we're using GL_SMOOTH, we need to calculate vertex normals for every vertex we use. If you need a refresher on normals in OpenGL, I have two previous blog postings on the topic here, and here.
So, in addition to an array of vertices, we need an array of vectors to hold our normals. Because we're calculating vertex normals, we need one vector for every vertex, so we need another array of the same size (vectors and vertices are represented by exactly the same data structure - in fact, my Vector3D is actually just #defined to a Vertex3D. Here's the array for the normals:
Vector3D flagVertexNormals;Calculating normals can be fairly costly - that's why OpenGL asks you to provide them rather than calculating them itself. So, we're going to cheat just like we did with the sine wave. We're going to simply shift the vertices over one. Because the relationship of each vertex to all of its neighbors stays the same, we don't have to recalculate the normals every frame, we can just calculate them once and keep re-using them by shifting them over the same way we will with the vertices.
Pre-calculating the vertex normals is not exactly straightforward however, because I've decided to use GL_TRIANGLE_STRIPs in this example, which should give better performance. So, each row of our vertex grid (except the last) is going to be used to build a triangle strip, our vertex strips are going to look like this:
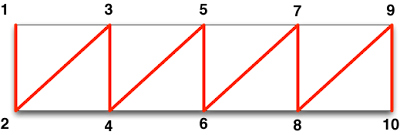
Triangle strips are very efficient - notice that we don't have to specify vertices more than once because OpenGL knows that triangles in a triangle strip share some vertices. To create the same shape using triangles would take twenty-four vertices (eight triangles by three vertices per triangle), as opposed to the ten it's taken us here. That's very cool, and whenever possible, you should use triangle strips (or triangle fans - a similar approach we'll discuss in a later blog posting) instead of triangles. It reduces the amount of geometry you need to submit to OpenGL in order to define a shape.
But, meshes made up of triangle strips are a bit of a pain when it comes to normals. If you remember: a vertex normal is the average of the surface normals for all the polygons that a vertex is used in. How many polygons is each vertex used in? Six, usually:

Usually. The outside strips on all four sides are special cases, and so are the four corners. Two of the corner vertices are only used in one triangle (the blue dot in the illustration below); the other two are used in two (the green dot in the illustration below). The rest of the triangles that make up the borders of the grid are each used in three triangles (like the red dot in the illustration below):

So, in our little grid here, we've got vertices that are used in six triangles, three triangles, two triangles, and one triangle. Yuck. Okay, this is going to be a little gnarly. Let's handle the typical scenario first - the non-edge, non-corner vertices which are shared by six triangles. We can loop through the rows and columns and calculate the vertex normals by calculating surface normals for the six triangles they are part of, we just have to skip the first and last row and column:
for (int x = 1; x < FLAG_X_POINTS-1; x++)
Okay, deep breath now, we'll get through this. Next, let's handle the top and bottom strips. We can do them in the same loop, we'll just ignore the first vertex when doing the top strip and the last vertex when doing the bottom, because those are special cases:
for (int x = 0; x < FLAG_X_POINTS; x++)
We do a similar thing for the left and right borders:
for (int y = 0; y < FLAG_Y_POINTS; y++)
And, finally, handle the four corners:
Vertex3D vertex1 = Triangle3DCalculateSurfaceNormal(Triangle3DMake(flagVertices, flagVertices, flagVertices));
Vertex3D vertex2 = Triangle3DCalculateSurfaceNormal(Triangle3DMake(flagVertices, flagVertices, flagVertices));
flagVertexNormals.x = (vertex1.x + vertex2.x) / 2.0;
flagVertexNormals.y = (vertex1.y + vertex2.y) / 2.0;
flagVertexNormals.z = (vertex1.z + vertex2.z) / 2.0;
vertex1 = Triangle3DCalculateSurfaceNormal(Triangle3DMake(flagVertices, flagVertices, flagVertices));
vertex2 = Triangle3DCalculateSurfaceNormal(Triangle3DMake(flagVertices, flagVertices, flagVertices));
flagVertexNormals.x = (vertex1.x + vertex2.x) / 2.0;
flagVertexNormals.y = (vertex1.y + vertex2.y) / 2.0;
flagVertexNormals.z = (vertex1.z + vertex2.z) / 2.0;
// Finally, top left and bottom right corners are part of one, so no averaging or normalzing needed
flagVertexNormals = Triangle3DCalculateSurfaceNormal(Triangle3DMake(flagVertices, flagVertices, flagVertices));
flagVertexNormals = Triangle3DCalculateSurfaceNormal(Triangle3DMake(flagVertices, flagVertices, flagVertices));When it comes time to draw in a few moments, we're going to submit the geometry to OpenGL once per triangle strip, so we need to allocate some memory to hold our vertex array, normal array, and texture coordinate array. Here are the variables that represent those objects - they are instance variables of my controller class:
Vertex3D *vertices;
GLfloat *texCoords;
Vector3D *normals;
GLuint stripVertexCount;And here's how we calculate the memory needed for each of these for one triangle strip:
stripVertexCount = ((FLAG_Y_POINTS - 1) * 2);
vertices = calloc(stripVertexCount, sizeof(Vertex3D));
texCoords = calloc(stripVertexCount, sizeof(GLfloat) * 4);
normals = calloc(stripVertexCount, sizeof(Vector3D));The reason that we use one less than the number of columns is that every time through the loop, we create triangles between one column and the next one, but we skip the last one because it will automatically get created the previous time through the loop (since each column creates triangles between itself and the next column). I know that's confusing, but look up at the first diagram - notice that there are ten vertices, but eight triangles? Try the math on that. There are five Y positions or columns in that diagram. If you subtract one from five, you get four. If you double four, you get eight, which is the number of triangles in that strip. Make sense?
The last thing we need to do in setup is to load the texture that we'll be mapping onto the flag. In this case, I've used a class I wrote for an earlier project to load a PVRTC-compressed texture. The iPhone has hardware support for PVRTC compression, so it's the best option in most cases, though I've heard reports from some people that the quality loss due to PVRTC compression makes it not suitable for all uses. In this case, it seems to work fine, so I've used it, though I also provide the uncompressed png of both textures in the project if you want to make changes, or just see if it looks any different without the compression.
OpenGLTexture3D *theTexture = ;
self.flagTexture = theTexture;
;Time to draw. In our drawView: method, which gets called on a timer to do the animation, we first clear the buffer. I've chosen to use a sky-blue color. We also set use glLoadIdentity() to cancel out any transformation that may be in place from previous drawing:
Next, I rotate the flag 90° so that it fits better on the screen. I could also have used autorotation to do this, but decided it was easier to just do a rotation transform. I also use a translate transform to move the flag back away from the camera so we can see it.
We need to make sure that some state is enabled so that we can use textures, coordinate arrays, vertex arrays, and normal arrays. In this project, we could have turned these on once in setupView: and just left them on, but it's good habit to wrap your code by turning on and off what you need, that way your code is more portable - you can drop this into some other OpenGL program and not worry about what is enabled elsewhere.
Next, I bind my texture to make sure that it uses the correct texture when it draws. Again, in this case, there is only one loaded texture, so this is unnecessary, but for portability sake, it's a good idea to bind your texture before you use it. I also fall back to using the default binding (of no texture) if my texture object happens to be nil:
if (flagTexture != nil)
;
else
;It's time to submit figure out the triangle strips and submit them to OpenGL:
int vertexCounter = 0;
int texCoordCounter = 0;
int normalCounter = 0;
for (int x = 0; x < FLAG_X_POINTS-1; x++)
There's a lot going on there. We're looping through the grid, creating triangle strips for each vertical row. We copy the vertices and the vertex normals from our pre-calculated array into the vertex array that we're going to submit to OpenGL. We keep re-using that same piece of memory for submitting every triangle strip, we just copy different data each time. You should be aware that there are more efficient ways of submitting geometry. We could submit a single array with all the vertices used (no duplicates) and then submit indices to the ones that make up each triangle strip. That's an optimization I'll show in a future blog posting, but I thought this code would be confusing enough without it.
After populating the vertex and normal arrays, we calculate the texture coordinates. Remember: OpenGL texture coordinates are floating point values from 0.0 to 1.0 that represent where each vertex is in relation to the entire bitmap image being used as a texture. We use two texture coordinates per triangle (lower left and upper right), and we calculate these by multiplying the current row or texture by one over the number of rows or columns. Pretty easy, actually.
Note: I'm actually cheating here. The flag is a rectangle, but textures on the iPhone need to be square. Rather than adjust the texture coordinates to account for that difference, I just took a rectangle and resized it to a square in photoshop, knowing that the distortion would be offset when it got compressed back onto the flag. I'm not necessarily suggesting you should do it that way in your real projects.
Next, we disable the features we're using. We don't have to do this, but it's a good idea - there might be code somewhere else that needs to draw without a texture, for example, and it won't necessarily know to turn this off.
And, finally, we move the values in the flag vertex and normal arrays over by one to make the flag wave.
for (int y =0 ; y< FLAG_Y_POINTS - 1; y++)
Don't expect to grok it all just from reading this. Go grab the Xcode project and look at the code, run it, make changes to it, and just generally play with it until you're comfortable with what it's doing. And if you come up with better ways of doing something, let me know, I'll post your code changes if I agree that they are better.
OpenGL ES's lack of direct mode can be a bit of an impediment to learning OpenGL. On the other hand, direct mode is really inefficient, and the technique we use on the iPhone will work on other OpenGL platforms, so, in the long run, it's really not a bad platform to learn on.







No comments:
Post a Comment