Tuesday, April 28, 2009
WWDC Has Sold Out
According to Matt Drance, Frameworks Evangelist at Apple, Elvis has left the building, and he took the last WWDC ticket with him. Hope you got your tickets, it gonna be swell.
Detecting a Circle Gesture
In Beginning iPhone Development, we have a chapter on gestures. While I think we covered the topic fairly well, I would have liked to have included a few more custom gestures in that chapter. By that point in writing, however, we were already way over on page count. Back then, we also just didn't have a good idea of what other gestures would become common.
I did experiment some with detecting circles back then, but didn't include the code in the book for two reasons. One reason is because the method is really quite long and would have taken a lot of explanation, which we didn't really have spare pages for. The second reasons is that I have a feeling there's a much easier and more efficient way to go about detecting a circle gesture. Because you need to build a certain amount of tolerance into gesture detection, I'm not sure that there is, but there's a least a decent chance there are better ways to detect a circle.
But, since a google search didn't turn up any sample code out there to do this, I decided I'd update the code and post it.
Please, if you see an easier way to do this and want to point it out, by all means, go for it.
You can download the sample project right here.
The sample app is very basic, it just traces the shape you draw and tells you either that it detected a circle, or tells you why it doesn't think the shape counts as a circle. I have not encapsulated this to be re-usable (yet, at least), but the technique is pretty self contained, requiring just three instance variables and overriding three of the touch handling methods. In the sample, the touch-handling code is in the view subclass, which made it easier to do the drawing, but the touch-handling should work in a view controller class as well.
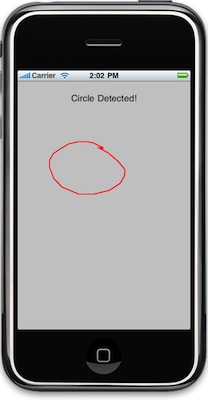
Here's a basic description of the algorithm I've used. You can download the code to see the exact implementation.
As I stated earlier, there's probably an easier, more accurate way to detect a circle, but until one comes to light, this is at least functional.
I did experiment some with detecting circles back then, but didn't include the code in the book for two reasons. One reason is because the method is really quite long and would have taken a lot of explanation, which we didn't really have spare pages for. The second reasons is that I have a feeling there's a much easier and more efficient way to go about detecting a circle gesture. Because you need to build a certain amount of tolerance into gesture detection, I'm not sure that there is, but there's a least a decent chance there are better ways to detect a circle.
But, since a google search didn't turn up any sample code out there to do this, I decided I'd update the code and post it.
Please, if you see an easier way to do this and want to point it out, by all means, go for it.
You can download the sample project right here.
The sample app is very basic, it just traces the shape you draw and tells you either that it detected a circle, or tells you why it doesn't think the shape counts as a circle. I have not encapsulated this to be re-usable (yet, at least), but the technique is pretty self contained, requiring just three instance variables and overriding three of the touch handling methods. In the sample, the touch-handling code is in the view subclass, which made it easier to do the drawing, but the touch-handling should work in a view controller class as well.

Here's a basic description of the algorithm I've used. You can download the code to see the exact implementation.
- In touchesBegan:withEvent: store the point where the user first tapped the screen
- In touchesMoved:withEvent: store off each additional touch point that comes in, storing them in order
- in touchesEnded:withEvent:, store the final point, then do a number of checks, doing the computationally cheap ones first so as to avoid having to do any of the more computationally expensive ones by ruling out obvious non-circles. Most of these checks are based on a variance or threshold defined in a constant:
- If the end point is too far away from the start point, it's not a circle.
- If the drawing operation took more than two seconds, it's not a circle. Okay, it might be a circle, but if it took too long, it's probably not an intentional gesture. You can remove this check if you don't want it.
- If there are not a certain number of stored points, it can't be a circle. This is to avoid false positives from lingering taps.
- Loop through the stored touches and determine the top-most, bottom-most, left-most, and right-most points, and use that to determine an approximate center and an approximate average radius.
- Loop through the stored points in order, making sure:
- Each point's distance from the center is within a certain variance of the approximate average radius.
- That the angle formed from the start point, to the radius, to the current point flows in a natural order. The angle should continuously increase or decrease. If it doesn't go in sequence, then it's probably a more complex shape than a circle.
As I stated earlier, there's probably an easier, more accurate way to detect a circle, but until one comes to light, this is at least functional.
iPhone Applications That Can Make Your Day
Many people around the world are currently rating the newest applications for IPhone. The Iphone phenomenon is extending rapidly and you are able to find thousands of opinions, comments and rankings everywhere on the web. Now, if you already have your IPhone, the next thing to do is find the proper apps that suit your needs. Most people tend to choose all those apps related to video, music and photos, because IPhone holds all kinds of entertainment in one…still, if you want it to be a part of your working life or of your life as a student and want to be virtually present everywhere too, here is a list of applications that can make your day.
1. Air Sharing: Left the information at home? Never again. No need to take your laptop everywhere. With this free app for file storage, you can transfer or exchange your files via wi-fi and carry them with you all the time. Files are accessed from the same program (compatibility with a huge amount of formats). Compatible with Mac, Windows and Linux.
2. Wikipanion plus: How many times have you needed a definition, a date, biography and other specific information and there is no PC around? With this Wikipedia browsing application for IPhone your problem is solved. All the knowledge from the web into a hand-sized gadget. Direct connection with Wikipedia servers, so there is no no third-party servers fuss. Automatic search while you type and the last visited page opens from when you last left the application. It supports searching and browsing in more than 75 languages. Great app!
3. Tweeter: Scaled down version of the Twitter for IPhone. You can update your status remotely, view direct messages sent to you or view the public timeline. Very nice interface. Upload images and show the world what you’re doing instantly. Great for sending a picture when words don’t seem to help for descriptions.
4. Skype: All Skype functionalities in your IPhone. You can call and chat with all your skype contacts. No extra voice delays (it uses an AJAX interface). If your contact is not online, you can still call his mobile or landline. Good for saving some money.
5. Fieldrunners: While commuting, a very good way to kill time and help your eyesight as well (games which involve lots of eye movement help distinguish contrast, a capacity that people start to lose as they grow older). This Tower Defense game has free content updates. The idea is to defend and control the field using a big selection of upgradeable towers and lots of tactics against your enemies (thousands!). Try to dominate the fieldrunners and rise to the top as the Tower Defense Master. Very entertaining and probably the best game for IPhone so far.
Technology is advancing so fast that I am sure that when this little article is published there will some new apps already in the market, waiting for new users and their ratings. In the meantime, let’s enjoy the good ones that we have already discovered which are making our lives a little more pleasant everyday.
Written by Josh Downing. You can find more of his articles at http://www.englishlci.com/
1. Air Sharing: Left the information at home? Never again. No need to take your laptop everywhere. With this free app for file storage, you can transfer or exchange your files via wi-fi and carry them with you all the time. Files are accessed from the same program (compatibility with a huge amount of formats). Compatible with Mac, Windows and Linux.
2. Wikipanion plus: How many times have you needed a definition, a date, biography and other specific information and there is no PC around? With this Wikipedia browsing application for IPhone your problem is solved. All the knowledge from the web into a hand-sized gadget. Direct connection with Wikipedia servers, so there is no no third-party servers fuss. Automatic search while you type and the last visited page opens from when you last left the application. It supports searching and browsing in more than 75 languages. Great app!
3. Tweeter: Scaled down version of the Twitter for IPhone. You can update your status remotely, view direct messages sent to you or view the public timeline. Very nice interface. Upload images and show the world what you’re doing instantly. Great for sending a picture when words don’t seem to help for descriptions.
4. Skype: All Skype functionalities in your IPhone. You can call and chat with all your skype contacts. No extra voice delays (it uses an AJAX interface). If your contact is not online, you can still call his mobile or landline. Good for saving some money.
5. Fieldrunners: While commuting, a very good way to kill time and help your eyesight as well (games which involve lots of eye movement help distinguish contrast, a capacity that people start to lose as they grow older). This Tower Defense game has free content updates. The idea is to defend and control the field using a big selection of upgradeable towers and lots of tactics against your enemies (thousands!). Try to dominate the fieldrunners and rise to the top as the Tower Defense Master. Very entertaining and probably the best game for IPhone so far.
Technology is advancing so fast that I am sure that when this little article is published there will some new apps already in the market, waiting for new users and their ratings. In the meantime, let’s enjoy the good ones that we have already discovered which are making our lives a little more pleasant everyday.
Written by Josh Downing. You can find more of his articles at http://www.englishlci.com/
Monday, April 27, 2009
Project Template Bugfix
If you've downloaded my OpenGL Xcode Project Template and are using it, you should re-download it. There's a potential crasher in there that's been fixed.
Surfing Facebook May Endanger Your Employment
The title of this post may sound slightly exaggerated, however losing a job was literally what has happened to an employee of a Swiss insurance company.
The story is simple and sad at the same time. The woman said she could not work in front of a computer as she needed to lie in the dark. However, she was then seen to be surfing the Facebook. This statement was made by her employer Nationale Suisse. This fact has destroyed the company's trust in the employee. As a result, the woman has been fired.
The fired woman says that she was indeed in bed and was surfing Facebook from her iPhone. Moreover, she accused her employer of spying on her and other employees by sending a mysterious friend request which allows access to personal online activity. Of course the company quickly rejected the accusations. According to the official information, employee's Facebook activity had been stumbled across by a colleague in November, before use of the social network site was blocked in the company.
What do you think about this story? Have your say in comments and don't forget to subscribe to our RSS and comments feeds.
Source: http://www.reuters.com/article/newsOne/idUSTRE53N4HH20090424
The story is simple and sad at the same time. The woman said she could not work in front of a computer as she needed to lie in the dark. However, she was then seen to be surfing the Facebook. This statement was made by her employer Nationale Suisse. This fact has destroyed the company's trust in the employee. As a result, the woman has been fired.
The fired woman says that she was indeed in bed and was surfing Facebook from her iPhone. Moreover, she accused her employer of spying on her and other employees by sending a mysterious friend request which allows access to personal online activity. Of course the company quickly rejected the accusations. According to the official information, employee's Facebook activity had been stumbled across by a colleague in November, before use of the social network site was blocked in the company.
What do you think about this story? Have your say in comments and don't forget to subscribe to our RSS and comments feeds.
Source: http://www.reuters.com/article/newsOne/idUSTRE53N4HH20090424
Saturday, April 25, 2009
OpenGL ES From the Ground Up, Part 3: Viewports in Perspective
Now that you got a taste of how to draw in OpenGL, let's take a step back and talk about something very important: the OpenGL viewport. Many people who are new to 3D programming, but who have worked with 3D graphics programs like Maya, Blender, or Lightwave, expect to find an object in OpenGL's virtual world called a "camera". There is no such beast. What there is, is a defined chunk of 3D space that can be seen. The virtual world is infinite, but computers don't deal well with infinite, so OpenGL asks us to define a chunk of space that can be seen by the viewer.
If we think of it in terms of the camera object that most 3D programs have, the middle of one end of the viewport is the camera. It's the point at which the viewer is standing. It's a virtual window into the virtual world. There is a certain amount of space that the viewer can see. She can't see stuff behind her. She can't see things outside of her angle of view. And she can't see things that are too far away. Think of the viewport as a shape determined by the parameters "what the viewer can see". That seems pretty straightforward, right?
Unfortunately, it is not. To explain why, we first need to talk about the fact that there are two different types of viewports that you can create in OpenGL ES: orthographic and perspective.
To understand this better, let's talk about railroad tracks, okay? Now, the two rails of a railroad track, in order to function correctly, have to be exactly a certain, unwavering distance apart. The exact distance varies with where the tracks are, and what type of train rides on them, but it's important that the rails (and the wheels on the train) be the same distance apart. If that weren't the case, trains simply wouldn't be able to function.
This fact is obvious if you look at railroad tracks from above.

But what happens if you stand on the railroad tracks and look down them. Don't say "you get hit by the train", I'm assuming you're smart enough to do this when the train's not coming.

Yeah, the tracks look like they get closer as they move away from us. That, as you're probably well aware thanks to your second grade art teacher, is due to something called perspective.
One of the two ways that OpenGL viewports can be set up is to use perspective. When you set up a viewport this way, objects will get smaller as they move away, and lines will converge as they move away from the viewer. This will simulate real vision; the way people see things in the real world.
The other way you can set up a view port is called an orthogonal viewport. In this type of viewport, lines never converge and things don't change in size. There is no perspective. This is handy for CAD programs and a number of other purposes, but it doesn't look real, because that's not the way our eyes work, so it's not usually what you want.
With an orthogonal viewport, you can put your virtual camera on the railroad tracks, but those rails will never converge. They will stay the same distance apart as they move away from you. Even if you defined an infinitely large viewport (which you can't do in OpenGL ES) those lines would stay the same distance apart.
The nice thing about orthogonal viewports is that they are easy to define. Since lines never diverge, you just define a chunk of the 3D world that looks like a box, like this:
You can tell OpenGL ES that you want to set up an orthogonal viewport by using the function glOrthof() before you set declare your viewport using the glViewport() function. Here's a simple example:
That's not really too difficult to understand. We first get our view's size. We make our chunk of space we're looking into two units wide, running from -1.0 to +1.0 on the x-axis. Easy enough.
Then, what's going on with the Bottom and Top? Well, we want the X and Y coordinates of our chunk of space to have the same aspect ratio as our view (which, in a full-screen app is the aspect ratio of the iPhone's screen). Since the iPhone's width and height are different, we need to make sure the x and y coordinates of our view are different also, in the same proportion.
After that, we define a near and far limit to delineate the depth of our viewing volume. The near parameter is where the viewport starts. If we're standing on the origin, the viewport starts right in front of it, so it's customary to use .01 or .001 as the start of an orthogonal viewport. This starts it a tiny fraction in "front" of the origin. The far coordinate can be set based on the needs of the application you're writing. If you'll never have an object further away than 20 units, you don't need to set a far of 20,000 units. Exactly what number you use is going to vary from program to program.
After the call to glOrthof(), we call glViewport() with the view's rectangle, and we're done.
That was the easy case.
Notice that as we move away from the viewpoint (in other words, as the value of z decreases), the viewing volume gets larger on both the x and y coordinates.
To set up a perspective viewport, we don't use glOrthof(), we use a different function called glFrustumf(). This method takes the same six parameters. That's easy enough to understand, but how do we figure out what numbers to pass into glFrustumf()?
Well, near and far are easy. You figure them out the same way. Use something like .001 for near, and then base far on the needs of your specific program.
But what about left, right, bottom, and top. To set those, we're going to need to do a little bit of math.
To calculate our frustum, we need to first figure out our field of vision, which is defined by two angles. Let's do this: Stick both of yours arm out straight in front of you, palms together. Your arms are now pointing down the z axis of your own personal frustum, right? Okay, now, move your hands apart slowly. Because your shoulders stay in the same position as your hands move apart, you're defining an increasingly large angle. This is one of the two angles that defines your own viewing frustum. This is the angle that defines the width of your field of view, the other would be if you did exactly the same thing but moved your apart up and down as opposed to left and right.. If your hands are three inches apart, the x-angle is pretty small.
A narrow field of vision.
If you move them two feet apart, you create a much wider angle, and a wider field of vision.
A wide field of vision.
If you're into photography, you can think of field of vision as the focal length of our virtual camera's virtual lens. A narrow field of vision is much like a telephoto lens, creating a long frustum that tapers slowly. A wide field of vision is like a wide angle lens and creates a frustum that increases in size much faster.
Let's pick a nice middle-of-the road value to start, say 45°. Now that we have this value, how do we use it to calculate our viewing frustum? Well, let's look at one of the two angles. Imagine, if you will, what the frustum looks like from the top. Heck, you don't have to imagine, here's a diagram:

Okay, from above, it looks kinda like a triangle, with just a little bit of one point lopped of, doesn't it? Well, it's close enough to a triangle for our purposes. Now, do you remember tangents from trig class? The tangent function is defined as the ratio of the opposite leg of a right triangle to the adjacent leg.

Okay, but we don't have a right triangle, do we?
Actually, we have two… if we draw a line right down the z axis:

That dotted line down the center is the "adjacent leg" of the two right triangles we just created by drawing that line. So, half of the width of the far end of the frustum is the tangent of half of the angle of our field of view. If we take that value and multiply it by the near value, we have the value to pass as right. We pass the inverse of that number as left.
We want our field of view to have the same aspect ratio as the screen, so we can calculate the top and bottom values exactly as we did with glOrthof() - by multiplying the right value by the screen's aspect ratio. In code, that would look like this:
Let's see it in action. I modified the final drawView: method from the last posting so that instead of one icosahedron, it shows thirty icosahedrons extending down the z axis. Here is the new drawView: method.
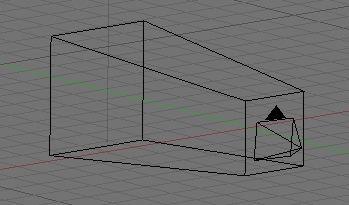
If you drop this code into a project created from OpenGL project template for Xcode, which sets up a perspective viewport using glFrustumf() with a 45° field of vision, you get something that looks like this:

Nice, right? They get smaller as they go away from you, very similar in appearance to those train tracks as they move away from you.
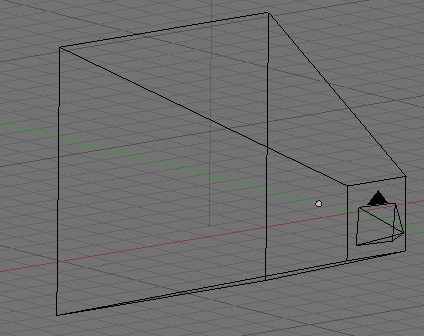
If we do nothing other than change the glFrustumf() call to a glOrthof() call, it looks much different:

Without perspective, the twenty-nine icosahedrons behind the first one are obscured by the first. There's no perspective, so each shape lies exactly behind the one in front of it on the z axis.
Okay, that was a heavy topic, and the truth of the matter is you can forget all about the trig now. Just copy the two lines of code that calculate a frustum based on an field of vision angle, and you will probably never need to remember why it works.
In the next installment, we're going to shine some light on our icosahedron and make it look like a real, honest-to-goodness three-dimensional shape rather than a colorful, but flat object.

If we think of it in terms of the camera object that most 3D programs have, the middle of one end of the viewport is the camera. It's the point at which the viewer is standing. It's a virtual window into the virtual world. There is a certain amount of space that the viewer can see. She can't see stuff behind her. She can't see things outside of her angle of view. And she can't see things that are too far away. Think of the viewport as a shape determined by the parameters "what the viewer can see". That seems pretty straightforward, right?
Unfortunately, it is not. To explain why, we first need to talk about the fact that there are two different types of viewports that you can create in OpenGL ES: orthographic and perspective.
Orthographic vs. Perspective
To understand this better, let's talk about railroad tracks, okay? Now, the two rails of a railroad track, in order to function correctly, have to be exactly a certain, unwavering distance apart. The exact distance varies with where the tracks are, and what type of train rides on them, but it's important that the rails (and the wheels on the train) be the same distance apart. If that weren't the case, trains simply wouldn't be able to function.
This fact is obvious if you look at railroad tracks from above.

But what happens if you stand on the railroad tracks and look down them. Don't say "you get hit by the train", I'm assuming you're smart enough to do this when the train's not coming.

Yeah, the tracks look like they get closer as they move away from us. That, as you're probably well aware thanks to your second grade art teacher, is due to something called perspective.
One of the two ways that OpenGL viewports can be set up is to use perspective. When you set up a viewport this way, objects will get smaller as they move away, and lines will converge as they move away from the viewer. This will simulate real vision; the way people see things in the real world.
The other way you can set up a view port is called an orthogonal viewport. In this type of viewport, lines never converge and things don't change in size. There is no perspective. This is handy for CAD programs and a number of other purposes, but it doesn't look real, because that's not the way our eyes work, so it's not usually what you want.
With an orthogonal viewport, you can put your virtual camera on the railroad tracks, but those rails will never converge. They will stay the same distance apart as they move away from you. Even if you defined an infinitely large viewport (which you can't do in OpenGL ES) those lines would stay the same distance apart.
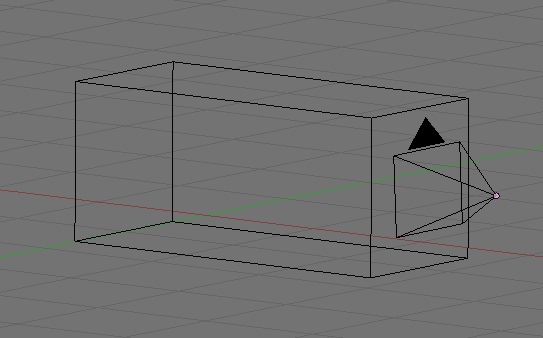
The nice thing about orthogonal viewports is that they are easy to define. Since lines never diverge, you just define a chunk of the 3D world that looks like a box, like this:

Setting up an Orthogonal Viewport
You can tell OpenGL ES that you want to set up an orthogonal viewport by using the function glOrthof() before you set declare your viewport using the glViewport() function. Here's a simple example:
CGRect rect = view.bounds;
glOrthof(-1.0, // Left
1.0, // Right
-1.0 / (rect.size.width / rect.size.height), // Bottom
1.0 / (rect.size.width / rect.size.height), // Top
0.01, // Near
10000.0); // Far
glViewport(0, 0, rect.size.width, rect.size.height);That's not really too difficult to understand. We first get our view's size. We make our chunk of space we're looking into two units wide, running from -1.0 to +1.0 on the x-axis. Easy enough.
Then, what's going on with the Bottom and Top? Well, we want the X and Y coordinates of our chunk of space to have the same aspect ratio as our view (which, in a full-screen app is the aspect ratio of the iPhone's screen). Since the iPhone's width and height are different, we need to make sure the x and y coordinates of our view are different also, in the same proportion.
After that, we define a near and far limit to delineate the depth of our viewing volume. The near parameter is where the viewport starts. If we're standing on the origin, the viewport starts right in front of it, so it's customary to use .01 or .001 as the start of an orthogonal viewport. This starts it a tiny fraction in "front" of the origin. The far coordinate can be set based on the needs of the application you're writing. If you'll never have an object further away than 20 units, you don't need to set a far of 20,000 units. Exactly what number you use is going to vary from program to program.
After the call to glOrthof(), we call glViewport() with the view's rectangle, and we're done.
That was the easy case.
Setting up the Perspective Viewport
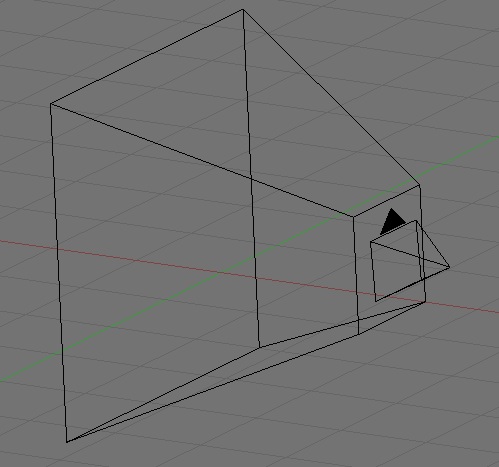
The other case is not quite as simple, and here's why. If objects get smaller as they move away from you, what does that do to the shape of the chunk of space you can see. You can see more of the world that's further away from you, so the chunk of space you need to define isn't a cube if you're using perspective. No, the shape of the space you can see when using perspective is called a frustum. Yeah, I know. Strange word, right? But it's a real thing. Our frustum will look something like this:
Notice that as we move away from the viewpoint (in other words, as the value of z decreases), the viewing volume gets larger on both the x and y coordinates.
To set up a perspective viewport, we don't use glOrthof(), we use a different function called glFrustumf(). This method takes the same six parameters. That's easy enough to understand, but how do we figure out what numbers to pass into glFrustumf()?
Well, near and far are easy. You figure them out the same way. Use something like .001 for near, and then base far on the needs of your specific program.
But what about left, right, bottom, and top. To set those, we're going to need to do a little bit of math.
To calculate our frustum, we need to first figure out our field of vision, which is defined by two angles. Let's do this: Stick both of yours arm out straight in front of you, palms together. Your arms are now pointing down the z axis of your own personal frustum, right? Okay, now, move your hands apart slowly. Because your shoulders stay in the same position as your hands move apart, you're defining an increasingly large angle. This is one of the two angles that defines your own viewing frustum. This is the angle that defines the width of your field of view, the other would be if you did exactly the same thing but moved your apart up and down as opposed to left and right.. If your hands are three inches apart, the x-angle is pretty small.

If you move them two feet apart, you create a much wider angle, and a wider field of vision.

If you're into photography, you can think of field of vision as the focal length of our virtual camera's virtual lens. A narrow field of vision is much like a telephoto lens, creating a long frustum that tapers slowly. A wide field of vision is like a wide angle lens and creates a frustum that increases in size much faster.
Let's pick a nice middle-of-the road value to start, say 45°. Now that we have this value, how do we use it to calculate our viewing frustum? Well, let's look at one of the two angles. Imagine, if you will, what the frustum looks like from the top. Heck, you don't have to imagine, here's a diagram:

Okay, from above, it looks kinda like a triangle, with just a little bit of one point lopped of, doesn't it? Well, it's close enough to a triangle for our purposes. Now, do you remember tangents from trig class? The tangent function is defined as the ratio of the opposite leg of a right triangle to the adjacent leg.
Okay, but we don't have a right triangle, do we?
Actually, we have two… if we draw a line right down the z axis:

That dotted line down the center is the "adjacent leg" of the two right triangles we just created by drawing that line. So, half of the width of the far end of the frustum is the tangent of half of the angle of our field of view. If we take that value and multiply it by the near value, we have the value to pass as right. We pass the inverse of that number as left.
We want our field of view to have the same aspect ratio as the screen, so we can calculate the top and bottom values exactly as we did with glOrthof() - by multiplying the right value by the screen's aspect ratio. In code, that would look like this:
CGRect rect = view.bounds;
GLfloat size = .01 * tanf(DEGREES_TO_RADIANS(45.0) / 2.0);
glFrustumf(-size, // Left
size, // Right
-size / (rect.size.width / rect.size.height), // Bottom
size / (rect.size.width / rect.size.height), // Top
.01, // Near
1000.0); // FarNote: A discussion of how glFrustum() uses the passed parameters to calculate the shape of the frustum going to have to wait until we've discussed matrices. For now, just take it on faith that this calculation works, okay?
Let's see it in action. I modified the final drawView: method from the last posting so that instead of one icosahedron, it shows thirty icosahedrons extending down the z axis. Here is the new drawView: method.
- (void)drawView:(GLView*)view;
{
static GLfloat rot = 0.0;
static const Vertex3D vertices[]= {
{0, -0.525731, 0.850651}, // vertices[0]
{0.850651, 0, 0.525731}, // vertices[1]
{0.850651, 0, -0.525731}, // vertices[2]
{-0.850651, 0, -0.525731}, // vertices[3]
{-0.850651, 0, 0.525731}, // vertices[4]
{-0.525731, 0.850651, 0}, // vertices[5]
{0.525731, 0.850651, 0}, // vertices[6]
{0.525731, -0.850651, 0}, // vertices[7]
{-0.525731, -0.850651, 0}, // vertices[8]
{0, -0.525731, -0.850651}, // vertices[9]
{0, 0.525731, -0.850651}, // vertices[10]
{0, 0.525731, 0.850651} // vertices[11]
};
static const Color3D colors[] = {
{1.0, 0.0, 0.0, 1.0},
{1.0, 0.5, 0.0, 1.0},
{1.0, 1.0, 0.0, 1.0},
{0.5, 1.0, 0.0, 1.0},
{0.0, 1.0, 0.0, 1.0},
{0.0, 1.0, 0.5, 1.0},
{0.0, 1.0, 1.0, 1.0},
{0.0, 0.5, 1.0, 1.0},
{0.0, 0.0, 1.0, 1.0},
{0.5, 0.0, 1.0, 1.0},
{1.0, 0.0, 1.0, 1.0},
{1.0, 0.0, 0.5, 1.0}
};
static const GLubyte icosahedronFaces[] = {
1, 2, 6,
1, 7, 2,
3, 4, 5,
4, 3, 8,
6, 5, 11,
5, 6, 10,
9, 10, 2,
10, 9, 3,
7, 8, 9,
8, 7, 0,
11, 0, 1,
0, 11, 4,
6, 2, 10,
1, 6, 11,
3, 5, 10,
5, 4, 11,
2, 7, 9,
7, 1, 0,
3, 9, 8,
4, 8, 0,
};
glLoadIdentity();
glClearColor(0.7, 0.7, 0.7, 1.0);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glEnableClientState(GL_VERTEX_ARRAY);
glEnableClientState(GL_COLOR_ARRAY);
glVertexPointer(3, GL_FLOAT, 0, vertices);
glColorPointer(4, GL_FLOAT, 0, colors);
for (int i = 1; i <= 30; i++)
{
glLoadIdentity();
glTranslatef(0.0f,-1.5,-3.0f * (GLfloat)i);
glRotatef(rot, 1.0, 1.0, 1.0);
glDrawElements(GL_TRIANGLES, 60, GL_UNSIGNED_BYTE, icosahedronFaces);
}
glDisableClientState(GL_VERTEX_ARRAY);
glDisableClientState(GL_COLOR_ARRAY);
static NSTimeInterval lastDrawTime;
if (lastDrawTime)
{
NSTimeInterval timeSinceLastDraw = [NSDate timeIntervalSinceReferenceDate] - lastDrawTime;
rot+=50 * timeSinceLastDraw;
}
lastDrawTime = [NSDate timeIntervalSinceReferenceDate];
}If you drop this code into a project created from OpenGL project template for Xcode, which sets up a perspective viewport using glFrustumf() with a 45° field of vision, you get something that looks like this:

Nice, right? They get smaller as they go away from you, very similar in appearance to those train tracks as they move away from you.
If we do nothing other than change the glFrustumf() call to a glOrthof() call, it looks much different:

Without perspective, the twenty-nine icosahedrons behind the first one are obscured by the first. There's no perspective, so each shape lies exactly behind the one in front of it on the z axis.
Okay, that was a heavy topic, and the truth of the matter is you can forget all about the trig now. Just copy the two lines of code that calculate a frustum based on an field of vision angle, and you will probably never need to remember why it works.
Stay tuned for next week's exciting adventure…
In the next installment, we're going to shine some light on our icosahedron and make it look like a real, honest-to-goodness three-dimensional shape rather than a colorful, but flat object.

Friday, April 24, 2009
Learn Cocoa Update
I just wanted to post a quick update about Learn Cocoa. Dave and I have gotten ourselves spread pretty thin. We have a number of projects in the pipeline for Apress, most of which we can't announce the details of yet.
Unfortunately, as a result, Learn Cocoa's publication date kept getting pushed further and further back. To remedy that, and to make sure we get a quality book to market in a reasonable timeframe, Dave and I have brought in a new principal author for Learn Cocoa. Jack Nutting has taken over the reins of the book, but Dave and I will still be involved with it. Jack's got a lot of Objective-C and Cocoa experience and Dave and I are both confident that it's going to be a great book.
In related news, we should be able to take the wraps off of our other projects by WWDC at the latest.
Unfortunately, as a result, Learn Cocoa's publication date kept getting pushed further and further back. To remedy that, and to make sure we get a quality book to market in a reasonable timeframe, Dave and I have brought in a new principal author for Learn Cocoa. Jack Nutting has taken over the reins of the book, but Dave and I will still be involved with it. Jack's got a lot of Objective-C and Cocoa experience and Dave and I are both confident that it's going to be a great book.
In related news, we should be able to take the wraps off of our other projects by WWDC at the latest.
Thursday, April 23, 2009
Using Instruments to check iPhone Texture Memory Usage
A great blog post for anyone doing OpenGL work on the iPhone.
via Noel of Snappy Touch, via Owen Goss of Streaming Colour, via Luke Lutman of zinc Row
via Noel of Snappy Touch, via Owen Goss of Streaming Colour, via Luke Lutman of zinc Row
Something to Make Apple Fan-Boys Turn Rhodamine (Pink)
An interesting discussion of someone's first experiences with Microsoft's Surface. I'm honestly a little saddened by this. I think nothing in the world could be better than good competition for Apple's touch-screen products, even if it's not a directly competing product, but if this account is anything to go buy, the Surface doesn't appear to be nipping at Apple's heels in any meaningful way. Oh, the product itself is okay, but the lack of attention to detail... well, it matters! Great technology isn't enough. If you miss the opportunity to wow with the first impression, you've got to fight very hard to get back in the user's good graces.
But, I must admit, there's a very small part of me - the Apple fan-boy part - that secretly smirks with satisfaction that Microsoft is yet again snatching defeat from the jaws of victory in another emerging market.
(via Dr. Wave)
But, I must admit, there's a very small part of me - the Apple fan-boy part - that secretly smirks with satisfaction that Microsoft is yet again snatching defeat from the jaws of victory in another emerging market.
(via Dr. Wave)
Another Fine Quarter
Yesterday, Apple announced another great quarter even in a tough economy. Although unit sales of Macs were down slightly, sales of both iPods and iPhone OS devices were up, and Apple called it "the best non-holiday quarter in Apple history".
One of the interesting tidbits of information that can be gleaned from the earnings report is the fact that there have now been 37 million iPhones and iPod Touches sold. Although there are probably some of those that aren't in service, the vast majority probably are still being used in some capacity.
So, yeah, the gold rush might be over (though I'm not entirely convinced about it), but it's still a hell of a market. To put that number in perspective, back in 2007, it was estimated that the installed base of Mac OS X computers was 22 million. Obviously that number is higher now - Apple sold 2.22 million Macs just in the past reporting quarter - but that means the potential market for iPhone applications today is considerably larger than the market for Mac programs was just two years ago.
The getting-rich-overnight stories may be coming to an end, but anyone who thinks the iPhone application market isn't still a great opportunity needs to have his or her head examined.
One of the interesting tidbits of information that can be gleaned from the earnings report is the fact that there have now been 37 million iPhones and iPod Touches sold. Although there are probably some of those that aren't in service, the vast majority probably are still being used in some capacity.
So, yeah, the gold rush might be over (though I'm not entirely convinced about it), but it's still a hell of a market. To put that number in perspective, back in 2007, it was estimated that the installed base of Mac OS X computers was 22 million. Obviously that number is higher now - Apple sold 2.22 million Macs just in the past reporting quarter - but that means the potential market for iPhone applications today is considerably larger than the market for Mac programs was just two years ago.
The getting-rich-overnight stories may be coming to an end, but anyone who thinks the iPhone application market isn't still a great opportunity needs to have his or her head examined.
Wednesday, April 22, 2009
Radial 50 - A New Take on the Arcade Legend
 I must admit that Breakout remains one of my favorite games of all time. After all, Breakout was the first game that I've played on a computer back in 1980s. From a programmer's perspective, Breakout is a sort of game (along with Columns of course) that every game programmer must develop. I've played all sorts and flavors of Break out from very traditional to very odd and sometimes bizarre versions.
I must admit that Breakout remains one of my favorite games of all time. After all, Breakout was the first game that I've played on a computer back in 1980s. From a programmer's perspective, Breakout is a sort of game (along with Columns of course) that every game programmer must develop. I've played all sorts and flavors of Break out from very traditional to very odd and sometimes bizarre versions.There is no doubt that iPhone has given the second life to the arcade game genre. While iPhone is a device with enough power to handle sophisticated 3D shooters, arcade is something that perfectly fits the wonder device. Accelerometer doesn't play the least role in this. It's a real pleasure and more action to play accelerometer-enabled games.
The folks at Roundthird have developed a cool Breakout-style game for iPhone called Radial 50. This is probably the most peculiar and novel variation of this game. "Radial 50 expands on the arcade classic by allowing players to control the paddle and ball around a 360-degree environment. The objective is different from the classic, as you are focused on defeating the central target rather than the often painful chore of eliminating all targets".
To admit I was sort of puzzled when I first heard about Radial 50. However, after watching the video I immediately admitted that Radial 50 would become one of the most addictive games for iPhone.
Radial 50 Demo from Radial 50 on Vimeo.
For now enjoy the video and stay tuned. Don't forget to subscribe to our RSS feed and follow us on Twitter or join our group at Facebook.
Monday, April 20, 2009
OpenGL ES From the Ground Up, Part 2: A Look at Simple Drawing
Okay, there's still a lot of theory to talk about, but before we spend too much time getting bogged down in complex math or difficult concepts, let's get our feet wet with some very basic drawing in OpenGL ES.
If you haven't already done so, grab a copy of my Empty OpenGL Xcode project template. We'll use this template as a starting point rather than Apple's provided one. You can install it by copying the unzipped folder to this location:
This template is designed for a full-screen OpenGL application, and has an OpenGL view and a corresponding view controller. The view is designed to be pretty hands-off and you shouldn't need to touch it most of the time. It handles some of the gnarley stuff we'll be talking about later on, like buffer swapping, but it calls out to its controller class for two things.
First, it calls out to the controller once when the view is being setup. The view controller's setupView: method gets called once to let the controller add any setup work it needs to do. This is where you would set up your viewport, add lights, and do other setup relevant to your project. For today, ignore that method. There's a very basic setup already in place that will let you do simple drawing. Which brings us to the other method.
The controller's drawView: method will get called at regular intervals based on the value of a constant called kRenderingFrequency. The initial value of this is 15.0, which means that drawView: will get called fifteen times a second. If you want to change the rendering frequency, you can find this constant defined in the file called ConstantsAndMacros.h.
For our first trick, let's add the following code to the existing drawView: method in GLViewController.m:
Before we talk about what's going on, go ahead and run it, and you should get something that looks like this:

It's a simple method; you could probably figure out what's going on if you try, but let's walk through it together. Since our method draws a triangle, we need three vertices, so we create three of those Vertex3D objects we talked about in the previous posting in this series:
You should notice that the z value for all three vertices is the same, and that that value (-3.0) is "behind" the origin. Because we haven't done anything to change it, we're looking into our virtual world as if we were standing on the origin, which is the default starting location. By placing the triangle at a z-position of -3, we ensure that we can see it on the screen.
After that, we create a Triangle3D object made up of those three vertices.
Now, that's pretty easy code to understand, right? But, behind the scenes, what it looks like to the computer is an array of 9 GLfloats. We could have accomplished the same thing by doing this:
Well, not quite exactly the same thing - there's one very minor but important difference. In our first example, we have to pass the address of our Triangle3D object into OpenGL (e.g. &triangle), but in the second example using the array, we'd simply pass in the array, because C arrays are pointers. But, don't worry too much about that, because this example will be the last time we declare a Triangle3D object this way. I'll explain why in a moment, but let's finish going through our code. The next thing we do is load the identity matrix. I'll devote at least one whole posting to transformation matrices, what they are and how they are used, but just think of this call as a "reset button" for OpenGL. It gets rid of any rotations, movement, or other changes to the virtual world and puts us back at the origin standing upright.
After that, we tell OpenGL that all drawing should be done over a light grey background. OpenGL generally expects colors to be defined using four clamped values. Remember from the previous post, clamped floats are floating point values that run from 0.0 to 1.0. So, we define colors by their red, green, and blue components, along with another component called alpha, which defines how much of what's behind the color shows through. Don't worry about alpha for now - for the time being, we'll just always set alpha to 1.0, which defines an opaque color.
To define white in OpenGL, we'd pass 1.0 for all four components. To define an opaque black, we'd pass 0.0 for the red, green, and blue components and 1.0 for alpha. The second line of code in that last example is the one that actually tells OpenGL to clear out anything that's been drawn before and erases everything to the clear color.
You're probably wondering what the two arguments to the glClear() call are. Well, again, we don't want to get too far ahead of ourselves, but those are constants that refer to values stored in a bitfield. OpenGL maintains a number of buffers, which are just chunks of memory used for different aspects of drawing. By logical or'ing these two particular values together, we tell OpenGL to clear two different buffers - the color buffer and the depth buffer. The color buffer stores the color for each pixel of the current frame. This is basically what you see on the screen. The depth buffer (sometimes also called the "z-buffer") holds information about how close or near the viewer each potential pixel is. It uses this information to determine whether a pixel needs to be drawn or not. Those are the two buffers you'll see most often in OpenGL. There are others, such as the stencil buffer and the accumulation buffer, but we're not going to talk about those, at least for a while. For now, just remember that before you draw a frame, you need to clear these two buffers so that the previous contents doesn't mess things up for you.
After that, we enable one of OpenGL's features called vertex arrays. This feature could probably just be turned on once in the setupView: method, but as a general rule, I like to enable and disable the functionality I use. You never know when another piece of code might be doing things differently. if you turn what you need on and then off again, the chances of problems are greatly reduced. In this example, say we had another class that didn't use vertex arrays to draw, but used vertex buffer objects instead. If either of the chunks of code left something enabled or didn't explicitly enable something they needed, one or both of the methods could end up with unexpected results.
The next thing we do is set the color that we're going to draw in. This line of code sets the drawing color to a bright red.
Now, all drawing done until another call to glColor4f() will be done using the color red. There are some exceptions to that, such as code that draws a textured shape, but basically, setting the color like this sets the color for all calls that follow it.
Since we're drawing with vertex arrays, we have to tell OpenGL where the array of vertices is. Remember, an array of vertices is just a C array of GLfloats, with each set of three values representing one vertex. We created a Triangle3D object, but in memory, it's exactly the same as nine consecutive GLfloats, so we can just pass in the address of the triangle.
The first parameter to glVertexPointer() indicates how many GLfloats represent each vertex. You can pass either 2 or 3 here depending on whether you're doing two-dimensional or three-dimensional drawing. Even though our object exists in a plane, we're drawing it in a three-dimensional virtual world and have defined it using three values per vertex, so we pass in 3 here. Next, we pass in an enum that tells OpenGL that our vertices are made up of GLfloats. They don't have to be - OpenGL ES is quite happy to let you use most any datatype in a vertex array, but it's rare to see anything other than GL_FLOAT. The next parameter... well, don't worry about the next parameter. That's a topic for future discussion. For now, it will always, always, always be 0. In a future posting, I'll show you how to use this parameter to interleave different types of data about the same object into a single data structure, but that's heavier juju than I'm ready to talk about now.
After that, we tell OpenGL to draw triangles between the vertices in the array we previously submitted.
As you probably guessed, the first parameter is an enum that tells OpenGL what to draw. Although OpenGL ES doesn't support quads or any other polygon besides triangles, it does still support a variety of drawing modes, including the ability do draw points, lines, line loops, triangle strips, and triangle fans. We'll talk about the various drawing modes later. For now, let's just stick with triangles.
Finally, we disable the one feature that we enabled earlier so we don't mess up other code elsewhere. Again, there is no other code in this example, but usually when you're using OpenGL, drawing is potentially happening from multiple objects.
And that's it. It works. It's not very impressive, and it's not very efficient, but it works. You're drawing in OpenGL. Yay! A certain number of times every second, this method is getting called, and it's drawing. Don't believe me? Add the following bold code to the method and run it again:
When you run it again, the triangle should slowly revolve around the origin. Don't worry too much about the mechanics of rotation, I just wanted to show you that your drawing code was getting called many times a second.
What if we want to draw a square? Well, OpenGL ES doesn't have squares, so we have to define a square out of triangles. That's easy enough to do - a square can be created out of two right triangles. How do we tweak the code above to draw two triangles, rather than one? Can we create two Triangle3Ds and submit those? Well, yeah, we could. But that would be inefficient. It would be better if we submitted both triangles as part of the same vertex array. We can do that by declaring an array of Triangle3D objects, or by allocating a chunk of memory that happens to be the same size as two Triangle3Ds or eighteen GLfloats.
Here's one way:
Run it now, and you should get something like this:

That code is less than ideal, however, because we're allocating our geometry on the stack, and we're causing a additional memory to be used because our Vertex3DMake() method creates a new Vertex3D on the stack, and then copies the values into the array.
For a simple example like this, that works fine, but in more complex cases, the geometry for defining 3D objects will be large enough that you don't want to be allocating it on the stack and you don't want to be allocating memory more than once for a given vertex, so it's a good idea to get in the habit of allocating your vertices on the heap by using our old friend malloc() (although I sometimes like to use calloc() instead because by setting all the values to zero, some errors are easier to track down). First, we need a function to set the values of an existing vertex instead of creating a new one the way Vertex3DMake() does. This'll work:
Now, here's the exact same code re-written to allocate the two triangles on the heap using this new function:
Okay, we've covered a lot of ground, but let's got a little further. Remember how I said that OpenGL ES has more than one drawing mode? Well, this square shape that currently requires 6 vertices (18 GLfloats) to draw can actually be drawn with just four vertices (12 GLfloats) using the drawing mode known as triangle strips (GL_TRIANGLE_STRIP).
Here's the basic idea behind a triangle strip: the first triangle in the strip is made up of the first three vertices (indexes 0, 1, 2). The second triangle is made up of two of the vertices from the previous triangle along with the next vertex in the array, and so on through the array. This picture might make more sense - the first triangle is vertices 1, 2, 3, the next is vertices 2, 3, 4, etc.:
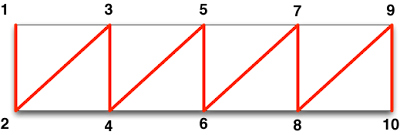
So, our square can be made like this:

The code to do it this way, looks like this:
Let's go to the first code sample to see something. Remember how we drew that first triangle? We used glColor4f() to set a color and said that it would set the color for all calls that follow. That means that every object defined in a vertex array has to be drawn in the same color? What? That's pretty limiting, isn't it?
Well, no. Just as OpenGL ES will allow you to pass vertices all at once in an array, it will also let you pass in a color array to specify the color to be used for each vertex. If you choose to use a color array, you need to have one color (four GLfloats) for each vertex. Color arrays have to be turned on using
Otherwise, the process is basically the same as passing in vertex arrays. We can use the same trick be defining a Color3D struct that contains four GLfloat members. Here's how you could pass in a different color for each array of that original triangle we drew:
If you run that, it should create a triangle that looks like this:

Let's look at one more thing today. One problem with the way we've been doing things is that if a vertex is used more than once (except in conjoining triangles in a triangle strip or triangle fan), you have to pass the same vertex into OpenGL multiple times. That's not a big deal, but you generally want to minimize the amount of data you're pushing into OpenGL, so pushing the same 4-byte floating point value over and over is less than ideal. In some meshes, a vertex could conceivably be used in seven or more different triangles, so your vertex array could be many times larger than it needs to be.
When dealing with these complex geometries, there's a way to avoid sending the same vertex multiple times, and it's by using something called elements to refer to vertices by their index in the vertex array. How this works is you'd create a vertex array that has each vertex once and only once. Then, you'd create another array of integers using the smallest unsigned integer datatype that will hold the number of unique vertices you have. In other words, if your vertex array has less than 256 vertices, then you would create an array of GLubytes, if it's more than 256, but less than 65,536, use GLushort. You build your triangles (or other shape) in this second array by referring to the vertices in the first array by their index. So, if you create vertices array with 12 vertices, then you refer to the first vertex in the array, you refer to as 0. You submit your vertices exactly the same way you did before, but instead of calling glDrawArrays(), you call a different function called glDrawElements() and pass in the integer array.
Let's finish our tutorial with a real, honest-to-goodness 3D shape: an icosahedron. Everybody else does cubes, but we're going to be geeky and do a twenty-sided die (sans numbers). Replace drawView: with this new version:
Before we talk about what's going on, let's run it and see the pretty shape spin:

It's not completely 3D looking because there are no lights and even if we had lights, we haven't told OpenGL what it needs to know to calculate how light should reflect off of our shape (that's a topic for a future posting - but if you want to, you can read some existing posts on the topic here and here).
So, what did we do here? First, we created a static variable to track the rotation of the object.
Then we defined our vertex array. We did it a little differently than before, but the result is the same. Since our geometry is not changing at all, we can make it const rather than allocating and deallocating memory every frame, and provide the values between curley braces:
Then we create a color array the same way. This creates an array of Color3D objects, one for each of the vertices in the previous array:
Finally, we create the array that actually defines the shape of the icosahedron. Those twelve vertices above, by themselves, don't describe this shape. OpenGL needs to know how to connect them, so for that, we create an array of integers (in this case GLubytes) that point to the vertices that make up each triangle.
So, the first three numbers in icosahedronFaces are 1,2,6, which means to draw a triangle between the vertices at indices 1 (0.850651, 0, 0.525731), 2 (0.850651, 0, 0.525731), and 6 (0.525731, 0.850651, 0).
The next chunk is nothing new, we just load the identity matrix (reset all transformations), move the shape away from the camera and rotate it, set the background color, clear the buffers, enable vertex and color arrays, then feed OpenGL our vertex array. All that is just like in some of the earlier examples.
But, then, we don't draw glDrawArrays(). We call glDrawElements():
After that, we just disable everything, and then increment the rotation variable based on how much time has elapsed since the last frame was drawn:
So, remember: if you provide the vertices in the right order to be drawn, you use glDrawArrays(), but if you provide an array of vertices and then a separate array of indices to identify the order they need to be drawn in, then you use glDrawElements().
Okay, that's enough for today. I covered a lot more ground than I intended to, and I probably got ahead of myself here, but hopefully this was helpful. In the next installment, we go back to conceptual stuff.
Please feel free to play with the drawing code, add more polygons, change colors, etc. There's a lot more to drawing in OpenGL than we covered here, but you've now seen the basic idea behind drawing 3D objects on the iPhone: You create a chunk of memory to hold all the vertices, pass the vertex array into OpenGL, and then tell it to draw those vertices.
If you haven't already done so, grab a copy of my Empty OpenGL Xcode project template. We'll use this template as a starting point rather than Apple's provided one. You can install it by copying the unzipped folder to this location:
/Developer/Platforms/iPhoneOS.platform/Developer/Library/Xcode/Project Templates/Application/
This template is designed for a full-screen OpenGL application, and has an OpenGL view and a corresponding view controller. The view is designed to be pretty hands-off and you shouldn't need to touch it most of the time. It handles some of the gnarley stuff we'll be talking about later on, like buffer swapping, but it calls out to its controller class for two things.
First, it calls out to the controller once when the view is being setup. The view controller's setupView: method gets called once to let the controller add any setup work it needs to do. This is where you would set up your viewport, add lights, and do other setup relevant to your project. For today, ignore that method. There's a very basic setup already in place that will let you do simple drawing. Which brings us to the other method.
The controller's drawView: method will get called at regular intervals based on the value of a constant called kRenderingFrequency. The initial value of this is 15.0, which means that drawView: will get called fifteen times a second. If you want to change the rendering frequency, you can find this constant defined in the file called ConstantsAndMacros.h.
For our first trick, let's add the following code to the existing drawView: method in GLViewController.m:
- (void)drawView:(GLView*)view;
{
Vertex3D vertex1 = Vertex3DMake(0.0, 1.0, -3.0);
Vertex3D vertex2 = Vertex3DMake(1.0, 0.0, -3.0);
Vertex3D vertex3 = Vertex3DMake(-1.0, 0.0, -3.0);
Triangle3D triangle = Triangle3DMake(vertex1, vertex2, vertex3);
glLoadIdentity();
glClearColor(0.7, 0.7, 0.7, 1.0);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glEnableClientState(GL_VERTEX_ARRAY);
glColor4f(1.0, 0.0, 0.0, 1.0);
glVertexPointer(3, GL_FLOAT, 0, &triangle);
glDrawArrays(GL_TRIANGLES, 0, 9);
glDisableClientState(GL_VERTEX_ARRAY);
}Before we talk about what's going on, go ahead and run it, and you should get something that looks like this:

It's a simple method; you could probably figure out what's going on if you try, but let's walk through it together. Since our method draws a triangle, we need three vertices, so we create three of those Vertex3D objects we talked about in the previous posting in this series:
Vertex3D vertex1 = Vertex3DMake(0.0, 1.0, -3.0);
Vertex3D vertex2 = Vertex3DMake(1.0, 0.0, -3.0);
Vertex3D vertex3 = Vertex3DMake(-1.0, 0.0, -3.0);You should notice that the z value for all three vertices is the same, and that that value (-3.0) is "behind" the origin. Because we haven't done anything to change it, we're looking into our virtual world as if we were standing on the origin, which is the default starting location. By placing the triangle at a z-position of -3, we ensure that we can see it on the screen.
After that, we create a Triangle3D object made up of those three vertices.
Triangle3D triangle = Triangle3DMake(vertex1, vertex2, vertex3);Now, that's pretty easy code to understand, right? But, behind the scenes, what it looks like to the computer is an array of 9 GLfloats. We could have accomplished the same thing by doing this:
GLfloat triangle[] = {0.0, 1.0, -3.0, 1.0, 0.0, -3.0, -1.0, 0.0, -3.0};Well, not quite exactly the same thing - there's one very minor but important difference. In our first example, we have to pass the address of our Triangle3D object into OpenGL (e.g. &triangle), but in the second example using the array, we'd simply pass in the array, because C arrays are pointers. But, don't worry too much about that, because this example will be the last time we declare a Triangle3D object this way. I'll explain why in a moment, but let's finish going through our code. The next thing we do is load the identity matrix. I'll devote at least one whole posting to transformation matrices, what they are and how they are used, but just think of this call as a "reset button" for OpenGL. It gets rid of any rotations, movement, or other changes to the virtual world and puts us back at the origin standing upright.
glLoadIdentity();After that, we tell OpenGL that all drawing should be done over a light grey background. OpenGL generally expects colors to be defined using four clamped values. Remember from the previous post, clamped floats are floating point values that run from 0.0 to 1.0. So, we define colors by their red, green, and blue components, along with another component called alpha, which defines how much of what's behind the color shows through. Don't worry about alpha for now - for the time being, we'll just always set alpha to 1.0, which defines an opaque color.
glClearColor(0.7, 0.7, 0.7, 1.0);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);To define white in OpenGL, we'd pass 1.0 for all four components. To define an opaque black, we'd pass 0.0 for the red, green, and blue components and 1.0 for alpha. The second line of code in that last example is the one that actually tells OpenGL to clear out anything that's been drawn before and erases everything to the clear color.
You're probably wondering what the two arguments to the glClear() call are. Well, again, we don't want to get too far ahead of ourselves, but those are constants that refer to values stored in a bitfield. OpenGL maintains a number of buffers, which are just chunks of memory used for different aspects of drawing. By logical or'ing these two particular values together, we tell OpenGL to clear two different buffers - the color buffer and the depth buffer. The color buffer stores the color for each pixel of the current frame. This is basically what you see on the screen. The depth buffer (sometimes also called the "z-buffer") holds information about how close or near the viewer each potential pixel is. It uses this information to determine whether a pixel needs to be drawn or not. Those are the two buffers you'll see most often in OpenGL. There are others, such as the stencil buffer and the accumulation buffer, but we're not going to talk about those, at least for a while. For now, just remember that before you draw a frame, you need to clear these two buffers so that the previous contents doesn't mess things up for you.
After that, we enable one of OpenGL's features called vertex arrays. This feature could probably just be turned on once in the setupView: method, but as a general rule, I like to enable and disable the functionality I use. You never know when another piece of code might be doing things differently. if you turn what you need on and then off again, the chances of problems are greatly reduced. In this example, say we had another class that didn't use vertex arrays to draw, but used vertex buffer objects instead. If either of the chunks of code left something enabled or didn't explicitly enable something they needed, one or both of the methods could end up with unexpected results.
glEnableClientState(GL_VERTEX_ARRAY);The next thing we do is set the color that we're going to draw in. This line of code sets the drawing color to a bright red.
glColor4f(1.0, 0.0, 0.0, 1.0);Now, all drawing done until another call to glColor4f() will be done using the color red. There are some exceptions to that, such as code that draws a textured shape, but basically, setting the color like this sets the color for all calls that follow it.
Since we're drawing with vertex arrays, we have to tell OpenGL where the array of vertices is. Remember, an array of vertices is just a C array of GLfloats, with each set of three values representing one vertex. We created a Triangle3D object, but in memory, it's exactly the same as nine consecutive GLfloats, so we can just pass in the address of the triangle.
glVertexPointer(3, GL_FLOAT, 0, &triangle);The first parameter to glVertexPointer() indicates how many GLfloats represent each vertex. You can pass either 2 or 3 here depending on whether you're doing two-dimensional or three-dimensional drawing. Even though our object exists in a plane, we're drawing it in a three-dimensional virtual world and have defined it using three values per vertex, so we pass in 3 here. Next, we pass in an enum that tells OpenGL that our vertices are made up of GLfloats. They don't have to be - OpenGL ES is quite happy to let you use most any datatype in a vertex array, but it's rare to see anything other than GL_FLOAT. The next parameter... well, don't worry about the next parameter. That's a topic for future discussion. For now, it will always, always, always be 0. In a future posting, I'll show you how to use this parameter to interleave different types of data about the same object into a single data structure, but that's heavier juju than I'm ready to talk about now.
After that, we tell OpenGL to draw triangles between the vertices in the array we previously submitted.
glDrawArrays(GL_TRIANGLES, 0, 9);As you probably guessed, the first parameter is an enum that tells OpenGL what to draw. Although OpenGL ES doesn't support quads or any other polygon besides triangles, it does still support a variety of drawing modes, including the ability do draw points, lines, line loops, triangle strips, and triangle fans. We'll talk about the various drawing modes later. For now, let's just stick with triangles.
Finally, we disable the one feature that we enabled earlier so we don't mess up other code elsewhere. Again, there is no other code in this example, but usually when you're using OpenGL, drawing is potentially happening from multiple objects.
glDisableClientState(GL_VERTEX_ARRAY);And that's it. It works. It's not very impressive, and it's not very efficient, but it works. You're drawing in OpenGL. Yay! A certain number of times every second, this method is getting called, and it's drawing. Don't believe me? Add the following bold code to the method and run it again:
- (void)drawView:(GLView*)view;
{
static GLfloat rotation = 0.0;
Vertex3D vertex1 = Vertex3DMake(0.0, 1.0, -3.0);
Vertex3D vertex2 = Vertex3DMake(1.0, 0.0, -3.0);
Vertex3D vertex3 = Vertex3DMake(-1.0, 0.0, -3.0);
Triangle3D triangle = Triangle3DMake(vertex1, vertex2, vertex3);
glLoadIdentity();
glRotatef(rotation, 0.0, 0.0, 1.0);
glClearColor(0.7, 0.7, 0.7, 1.0);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glEnableClientState(GL_VERTEX_ARRAY);
glColor4f(1.0, 0.0, 0.0, 1.0);
glVertexPointer(3, GL_FLOAT, 0, &triangle);
glDrawArrays(GL_TRIANGLES, 0, 9);
glDisableClientState(GL_VERTEX_ARRAY);
rotation+= 0.5;
}When you run it again, the triangle should slowly revolve around the origin. Don't worry too much about the mechanics of rotation, I just wanted to show you that your drawing code was getting called many times a second.
What if we want to draw a square? Well, OpenGL ES doesn't have squares, so we have to define a square out of triangles. That's easy enough to do - a square can be created out of two right triangles. How do we tweak the code above to draw two triangles, rather than one? Can we create two Triangle3Ds and submit those? Well, yeah, we could. But that would be inefficient. It would be better if we submitted both triangles as part of the same vertex array. We can do that by declaring an array of Triangle3D objects, or by allocating a chunk of memory that happens to be the same size as two Triangle3Ds or eighteen GLfloats.
Here's one way:
- (void)drawView:(GLView*)view;
{
Triangle3D triangle[2];
triangle[0].v1 = Vertex3DMake(0.0, 1.0, -3.0);
triangle[0].v2 = Vertex3DMake(1.0, 0.0, -3.0);
triangle[0].v3 = Vertex3DMake(-1.0, 0.0, -3.0);
triangle[1].v1 = Vertex3DMake(-1.0, 0.0, -3.0);
triangle[1].v2 = Vertex3DMake(1.0, 0.0, -3.0);
triangle[1].v3 = Vertex3DMake(0.0, -1.0, -3.0);
glLoadIdentity();
glClearColor(0.7, 0.7, 0.7, 1.0);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glEnableClientState(GL_VERTEX_ARRAY);
glColor4f(1.0, 0.0, 0.0, 1.0);
glVertexPointer(3, GL_FLOAT, 0, &triangle);
glDrawArrays(GL_TRIANGLES, 0, 18);
glDisableClientState(GL_VERTEX_ARRAY);
}Run it now, and you should get something like this:

That code is less than ideal, however, because we're allocating our geometry on the stack, and we're causing a additional memory to be used because our Vertex3DMake() method creates a new Vertex3D on the stack, and then copies the values into the array.
For a simple example like this, that works fine, but in more complex cases, the geometry for defining 3D objects will be large enough that you don't want to be allocating it on the stack and you don't want to be allocating memory more than once for a given vertex, so it's a good idea to get in the habit of allocating your vertices on the heap by using our old friend malloc() (although I sometimes like to use calloc() instead because by setting all the values to zero, some errors are easier to track down). First, we need a function to set the values of an existing vertex instead of creating a new one the way Vertex3DMake() does. This'll work:
static inline void Vertex3DSet(Vertex3D *vertex, CGFloat inX, CGFloat inY, CGFloat inZ)
{
vertex->x = inX;
vertex->y = inY;
vertex->z = inZ;
}Now, here's the exact same code re-written to allocate the two triangles on the heap using this new function:
- (void)drawView:(GLView*)view;
{
Triangle3D *triangles = malloc(sizeof(Triangle3D) * 2);
Vertex3DSet(&triangles[0].v1, 0.0, 1.0, -3.0);
Vertex3DSet(&triangles[0].v2, 1.0, 0.0, -3.0);
Vertex3DSet(&triangles[0].v3, -1.0, 0.0, -3.0);
Vertex3DSet(&triangles[1].v1, -1.0, 0.0, -3.0);
Vertex3DSet(&triangles[1].v2, 1.0, 0.0, -3.0);
Vertex3DSet(&triangles[1].v3, 0.0, -1.0, -3.0);
glLoadIdentity();
glClearColor(0.7, 0.7, 0.7, 1.0);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glEnableClientState(GL_VERTEX_ARRAY);
glColor4f(1.0, 0.0, 0.0, 1.0);
glVertexPointer(3, GL_FLOAT, 0, triangles);
glDrawArrays(GL_TRIANGLES, 0, 18);
glDisableClientState(GL_VERTEX_ARRAY);
if (triangles != NULL)
free(triangles);
}Okay, we've covered a lot of ground, but let's got a little further. Remember how I said that OpenGL ES has more than one drawing mode? Well, this square shape that currently requires 6 vertices (18 GLfloats) to draw can actually be drawn with just four vertices (12 GLfloats) using the drawing mode known as triangle strips (GL_TRIANGLE_STRIP).
Here's the basic idea behind a triangle strip: the first triangle in the strip is made up of the first three vertices (indexes 0, 1, 2). The second triangle is made up of two of the vertices from the previous triangle along with the next vertex in the array, and so on through the array. This picture might make more sense - the first triangle is vertices 1, 2, 3, the next is vertices 2, 3, 4, etc.:

So, our square can be made like this:

The code to do it this way, looks like this:
- (void)drawView:(GLView*)view;
{
Vertex3D *vertices = malloc(sizeof(Vertex3D) * 4);
Vertex3DSet(&vertices[0], 0.0, 1.0, -3.0);
Vertex3DSet(&vertices[1], 1.0, 0.0, -3.0);
Vertex3DSet(&vertices[2], -1.0, 0.0, -3.0);
Vertex3DSet(&vertices[3], 0.0, -1.0, -3.0);
glLoadIdentity();
glClearColor(0.7, 0.7, 0.7, 1.0);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glEnableClientState(GL_VERTEX_ARRAY);
glColor4f(1.0, 0.0, 0.0, 1.0);
glVertexPointer(3, GL_FLOAT, 0, vertices);
glDrawArrays(GL_TRIANGLE_STRIP, 0, 12);
glDisableClientState(GL_VERTEX_ARRAY);
if (vertices != NULL)
free(vertices);
}Let's go to the first code sample to see something. Remember how we drew that first triangle? We used glColor4f() to set a color and said that it would set the color for all calls that follow. That means that every object defined in a vertex array has to be drawn in the same color? What? That's pretty limiting, isn't it?
Well, no. Just as OpenGL ES will allow you to pass vertices all at once in an array, it will also let you pass in a color array to specify the color to be used for each vertex. If you choose to use a color array, you need to have one color (four GLfloats) for each vertex. Color arrays have to be turned on using
glEnableClientState(GL_COLOR_ARRAY);
Otherwise, the process is basically the same as passing in vertex arrays. We can use the same trick be defining a Color3D struct that contains four GLfloat members. Here's how you could pass in a different color for each array of that original triangle we drew:
- (void)drawView:(GLView*)view;
{
Vertex3D vertex1 = Vertex3DMake(0.0, 1.0, -3.0);
Vertex3D vertex2 = Vertex3DMake(1.0, 0.0, -3.0);
Vertex3D vertex3 = Vertex3DMake(-1.0, 0.0, -3.0);
Triangle3D triangle = Triangle3DMake(vertex1, vertex2, vertex3);
Color3D *colors = malloc(sizeof(Color3D) * 3);
Color3DSet(&colors[0], 1.0, 0.0, 0.0, 1.0);
Color3DSet(&colors[1], 0.0, 1.0, 0.0, 1.0);
Color3DSet(&colors[2], 0.0, 0.0, 1.0, 1.0);
glLoadIdentity();
glClearColor(0.7, 0.7, 0.7, 1.0);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glEnableClientState(GL_VERTEX_ARRAY);
glEnableClientState(GL_COLOR_ARRAY);
glColor4f(1.0, 0.0, 0.0, 1.0);
glVertexPointer(3, GL_FLOAT, 0, &triangle);
glColorPointer(4, GL_FLOAT, 0, colors);
glDrawArrays(GL_TRIANGLES, 0, 9);
glDisableClientState(GL_VERTEX_ARRAY);
glDisableClientState(GL_COLOR_ARRAY);
if (colors != NULL)
free(colors);
}If you run that, it should create a triangle that looks like this:

Let's look at one more thing today. One problem with the way we've been doing things is that if a vertex is used more than once (except in conjoining triangles in a triangle strip or triangle fan), you have to pass the same vertex into OpenGL multiple times. That's not a big deal, but you generally want to minimize the amount of data you're pushing into OpenGL, so pushing the same 4-byte floating point value over and over is less than ideal. In some meshes, a vertex could conceivably be used in seven or more different triangles, so your vertex array could be many times larger than it needs to be.
When dealing with these complex geometries, there's a way to avoid sending the same vertex multiple times, and it's by using something called elements to refer to vertices by their index in the vertex array. How this works is you'd create a vertex array that has each vertex once and only once. Then, you'd create another array of integers using the smallest unsigned integer datatype that will hold the number of unique vertices you have. In other words, if your vertex array has less than 256 vertices, then you would create an array of GLubytes, if it's more than 256, but less than 65,536, use GLushort. You build your triangles (or other shape) in this second array by referring to the vertices in the first array by their index. So, if you create vertices array with 12 vertices, then you refer to the first vertex in the array, you refer to as 0. You submit your vertices exactly the same way you did before, but instead of calling glDrawArrays(), you call a different function called glDrawElements() and pass in the integer array.
Let's finish our tutorial with a real, honest-to-goodness 3D shape: an icosahedron. Everybody else does cubes, but we're going to be geeky and do a twenty-sided die (sans numbers). Replace drawView: with this new version:
- (void)drawView:(GLView*)view;
{
static GLfloat rot = 0.0;
// This is the same result as using Vertex3D, just faster to type and
// can be made const this way
static const Vertex3D vertices[]= {
{0, -0.525731, 0.850651}, // vertices[0]
{0.850651, 0, 0.525731}, // vertices[1]
{0.850651, 0, -0.525731}, // vertices[2]
{-0.850651, 0, -0.525731}, // vertices[3]
{-0.850651, 0, 0.525731}, // vertices[4]
{-0.525731, 0.850651, 0}, // vertices[5]
{0.525731, 0.850651, 0}, // vertices[6]
{0.525731, -0.850651, 0}, // vertices[7]
{-0.525731, -0.850651, 0}, // vertices[8]
{0, -0.525731, -0.850651}, // vertices[9]
{0, 0.525731, -0.850651}, // vertices[10]
{0, 0.525731, 0.850651} // vertices[11]
};
static const Color3D colors[] = {
{1.0, 0.0, 0.0, 1.0},
{1.0, 0.5, 0.0, 1.0},
{1.0, 1.0, 0.0, 1.0},
{0.5, 1.0, 0.0, 1.0},
{0.0, 1.0, 0.0, 1.0},
{0.0, 1.0, 0.5, 1.0},
{0.0, 1.0, 1.0, 1.0},
{0.0, 0.5, 1.0, 1.0},
{0.0, 0.0, 1.0, 1.0},
{0.5, 0.0, 1.0, 1.0},
{1.0, 0.0, 1.0, 1.0},
{1.0, 0.0, 0.5, 1.0}
};
static const GLubyte icosahedronFaces[] = {
1, 2, 6,
1, 7, 2,
3, 4, 5,
4, 3, 8,
6, 5, 11,
5, 6, 10,
9, 10, 2,
10, 9, 3,
7, 8, 9,
8, 7, 0,
11, 0, 1,
0, 11, 4,
6, 2, 10,
1, 6, 11,
3, 5, 10,
5, 4, 11,
2, 7, 9,
7, 1, 0,
3, 9, 8,
4, 8, 0,
};
glLoadIdentity();
glTranslatef(0.0f,0.0f,-3.0f);
glRotatef(rot,1.0f,1.0f,1.0f);
glClearColor(0.7, 0.7, 0.7, 1.0);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glEnableClientState(GL_VERTEX_ARRAY);
glEnableClientState(GL_COLOR_ARRAY);
glVertexPointer(3, GL_FLOAT, 0, vertices);
glColorPointer(4, GL_FLOAT, 0, colors);
glDrawElements(GL_TRIANGLES, 60, GL_UNSIGNED_BYTE, icosahedronFaces);
glDisableClientState(GL_VERTEX_ARRAY);
glDisableClientState(GL_COLOR_ARRAY);
static NSTimeInterval lastDrawTime;
if (lastDrawTime)
{
NSTimeInterval timeSinceLastDraw = [NSDate timeIntervalSinceReferenceDate] - lastDrawTime;
rot+=50 * timeSinceLastDraw;
}
lastDrawTime = [NSDate timeIntervalSinceReferenceDate];
}Before we talk about what's going on, let's run it and see the pretty shape spin:

It's not completely 3D looking because there are no lights and even if we had lights, we haven't told OpenGL what it needs to know to calculate how light should reflect off of our shape (that's a topic for a future posting - but if you want to, you can read some existing posts on the topic here and here).
So, what did we do here? First, we created a static variable to track the rotation of the object.
static GLfloat rot = 0.0;Then we defined our vertex array. We did it a little differently than before, but the result is the same. Since our geometry is not changing at all, we can make it const rather than allocating and deallocating memory every frame, and provide the values between curley braces:
static const Vertex3D vertices[]= {
{0, -0.525731, 0.850651}, // vertices[0]
{0.850651, 0, 0.525731}, // vertices[1]
{0.850651, 0, -0.525731}, // vertices[2]
{-0.850651, 0, -0.525731}, // vertices[3]
{-0.850651, 0, 0.525731}, // vertices[4]
{-0.525731, 0.850651, 0}, // vertices[5]
{0.525731, 0.850651, 0}, // vertices[6]
{0.525731, -0.850651, 0}, // vertices[7]
{-0.525731, -0.850651, 0}, // vertices[8]
{0, -0.525731, -0.850651}, // vertices[9]
{0, 0.525731, -0.850651}, // vertices[10]
{0, 0.525731, 0.850651} // vertices[11]
};Then we create a color array the same way. This creates an array of Color3D objects, one for each of the vertices in the previous array:
static const Color3D colors[] = {
{1.0, 0.0, 0.0, 1.0},
{1.0, 0.5, 0.0, 1.0},
{1.0, 1.0, 0.0, 1.0},
{0.5, 1.0, 0.0, 1.0},
{0.0, 1.0, 0.0, 1.0},
{0.0, 1.0, 0.5, 1.0},
{0.0, 1.0, 1.0, 1.0},
{0.0, 0.5, 1.0, 1.0},
{0.0, 0.0, 1.0, 1.0},
{0.5, 0.0, 1.0, 1.0},
{1.0, 0.0, 1.0, 1.0},
{1.0, 0.0, 0.5, 1.0}
};Finally, we create the array that actually defines the shape of the icosahedron. Those twelve vertices above, by themselves, don't describe this shape. OpenGL needs to know how to connect them, so for that, we create an array of integers (in this case GLubytes) that point to the vertices that make up each triangle.
static const GLubyte icosahedronFaces[] = {
1, 2, 6,
1, 7, 2,
3, 4, 5,
4, 3, 8,
6, 5, 11,
5, 6, 10,
9, 10, 2,
10, 9, 3,
7, 8, 9,
8, 7, 0,
11, 0, 1,
0, 11, 4,
6, 2, 10,
1, 6, 11,
3, 5, 10,
5, 4, 11,
2, 7, 9,
7, 1, 0,
3, 9, 8,
4, 8, 0,
};So, the first three numbers in icosahedronFaces are 1,2,6, which means to draw a triangle between the vertices at indices 1 (0.850651, 0, 0.525731), 2 (0.850651, 0, 0.525731), and 6 (0.525731, 0.850651, 0).
The next chunk is nothing new, we just load the identity matrix (reset all transformations), move the shape away from the camera and rotate it, set the background color, clear the buffers, enable vertex and color arrays, then feed OpenGL our vertex array. All that is just like in some of the earlier examples.
glLoadIdentity();
glTranslatef(0.0f,0.0f,-3.0f);
glRotatef(rot,1.0f,1.0f,1.0f);
glClearColor(0.7, 0.7, 0.7, 1.0);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glEnableClientState(GL_VERTEX_ARRAY);
glEnableClientState(GL_COLOR_ARRAY);
glColor4f(1.0, 0.0, 0.0, 1.0);
glVertexPointer(3, GL_FLOAT, 0, vertices);
glColorPointer(4, GL_FLOAT, 0, colors);But, then, we don't draw glDrawArrays(). We call glDrawElements():
glDrawElements(GL_TRIANGLES, 60, GL_UNSIGNED_BYTE, icosahedronFaces);After that, we just disable everything, and then increment the rotation variable based on how much time has elapsed since the last frame was drawn:
glDisableClientState(GL_VERTEX_ARRAY);
glDisableClientState(GL_COLOR_ARRAY);
static NSTimeInterval lastDrawTime;
if (lastDrawTime)
{
NSTimeInterval timeSinceLastDraw = [NSDate timeIntervalSinceReferenceDate] - lastDrawTime;
rot+=50 * timeSinceLastDraw;
}
lastDrawTime = [NSDate timeIntervalSinceReferenceDate];So, remember: if you provide the vertices in the right order to be drawn, you use glDrawArrays(), but if you provide an array of vertices and then a separate array of indices to identify the order they need to be drawn in, then you use glDrawElements().
Okay, that's enough for today. I covered a lot more ground than I intended to, and I probably got ahead of myself here, but hopefully this was helpful. In the next installment, we go back to conceptual stuff.
Please feel free to play with the drawing code, add more polygons, change colors, etc. There's a lot more to drawing in OpenGL than we covered here, but you've now seen the basic idea behind drawing 3D objects on the iPhone: You create a chunk of memory to hold all the vertices, pass the vertex array into OpenGL, and then tell it to draw those vertices.
Subscribe to:
Comments (Atom)