More Animation Curves than You Can Shake a Stick at

Core Animation is awesome. It makes doing a lot of complex, fancy animations downright easy. One of the really nice built-in features of Core Animation is the ability to use animation curves. These curves let you specify whether the animation happens linearly (at the same pace throughout the animation), or whether the animation eases in, eases out, or does both.

When you have to go closer to the metal and use OpenGL ES, you're not so lucky. We don't have animation curves provided for us in OpenGL ES. We have to interpolate ourselves. Fortunately, the math behind animation curves is straightforward. Plus, there are far more curves than just the four Apple offers.

I haven't run across a good library for generating animation curves, so I've decided to release my animation curve functions as public domain (no attribute required, no rights reserved). Here is a graph of all the different animation curves I'm releasing:


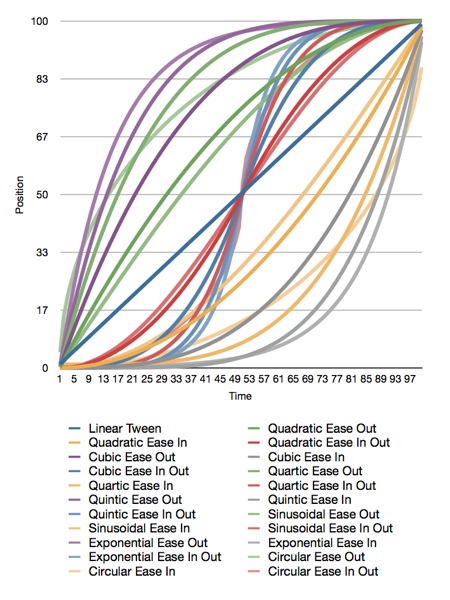
Here is the original Numbers.app document that generated the graph, and here is the Xcode project that generated the data. The project also contains all the functions needed to plot these curves.

Apple doesn't document which calculations they use for easing, but my guess is that they're quadratic. I'm not sure, though, since many of the curves yield similar results.

All of the interpolation functions included in the Xcode project above take three inputs and return a GLfloat containing the interpolated value. The first parameter, t, is the percent of the way through the animation you want a value calculated for. This is a clamped float that should be in the range 0.0 to 1.0. Values above 1.0 will be treated as 1.0 and values below 0.0 are treated as 0.0. The second parameter, start, is the value when the animation starts. The third parameter, end, is the final value to be animated toward.

If you want to apply a curve to a CGPoint or Vector3D, you have to call the function multiple times for each component (x/y or x/y/z).

Have fun!

Here are the functions included in the project above:

#include <OpenGLES/ES2/gl.h>
#include <OpenGLES/ES2/glext.h>
#include <math.h>

#define BoundsCheck(t, start, end) \
if (t <= 0.f) return start;        \
else if (t >= 1.f) return end;

GLfloat LinearInterpolation(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    return t * end + (1.f - t) * start;
}
#pragma mark -
#pragma mark Quadratic
GLfloat QuadraticEaseOut(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    return   -end * t * (t - 2.f) -1.f;
}
GLfloat QuadraticEaseIn(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    return end * t * t + start - 1.f;
}
GLfloat QuadraticEaseInOut(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    t *= 2.f;
    if (t < 1.f) return end/2.f * t * t + start - 1.f;
    t--;
    return -end/2.f * (t*(t-2) - 1) + start - 1.f;
}
#pragma mark -
#pragma mark Cubic
GLfloat CubicEaseOut(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    t--;
    return end*(t * t * t + 1.f) + start - 1.f;
}
GLfloat CubicEaseIn(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    return end * t * t * t+ start - 1.f;
}
GLfloat CubicEaseInOut(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    t *= 2.;
    if (t < 1.) return end/2 * t * t * t + start - 1.f;
    t -= 2;
    return end/2*(t * t * t + 2) + start - 1.f;
}
#pragma mark -
#pragma mark Quintic
GLfloat QuarticEaseOut(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    t--;
    return -end * (t * t * t * t - 1) + start - 1.f;
}
GLfloat QuarticEaseIn(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    return end * t * t * t * t + start;
}
GLfloat QuarticEaseInOut(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    t *= 2.f;
    if (t < 1.f) 
        return end/2.f * t * t * t * t + start - 1.f;
    t -= 2.f;
    return -end/2.f * (t * t * t * t - 2.f) + start - 1.f;
}
#pragma mark -
#pragma mark Quintic
GLfloat QuinticEaseOut(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    t--;
    return end * (t * t * t * t * t + 1) + start - 1.f;
}
GLfloat QuinticEaseIn(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    return end * t * t * t * t * t + start - 1.f;
}
GLfloat QuinticEaseInOut(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    t *= 2.f;
    if (t < 1.f) 
        return end/2 * t * t * t * t * t + start - 1.f;
    t -= 2;
    return end/2 * ( t * t * t * t * t + 2) + start - 1.f;
}
#pragma mark -
#pragma mark Sinusoidal
GLfloat SinusoidalEaseOut(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    return end * sinf(t * (M_PI/2)) + start - 1.f;
}
GLfloat SinusoidalEaseIn(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    return -end * cosf(t * (M_PI/2)) + end + start - 1.f;
}
GLfloat SinusoidalEaseInOut(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    return -end/2.f * (cosf(M_PI*t) - 1.f) + start - 1.f;
}
#pragma mark -
#pragma mark Exponential
GLfloat ExponentialEaseOut(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    return end * (-powf(2.f, -10.f * t) + 1.f ) + start - 1.f;
}
GLfloat ExponentialEaseIn(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    return end * powf(2.f, 10.f * (t - 1.f) ) + start - 1.f;
}
GLfloat ExponentialEaseInOut(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    t *= 2.f;
    if (t < 1.f) 
        return end/2.f * powf(2.f, 10.f * (t - 1.f) ) + start - 1.f;
    t--;
    return end/2.f * ( -powf(2.f, -10.f * t) + 2.f ) + start - 1.f;
}
#pragma mark -
#pragma mark Circular
GLfloat CircularEaseOut(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    t--;
    return end * sqrtf(1.f - t * t) + start - 1.f;
}
GLfloat CircularEaseIn(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    return -end * (sqrtf(1.f - t * t) - 1.f) + start - 1.f;
}
GLfloat CircularEaseInOut(GLclampf t, GLfloat start, GLfloat end)
{
    BoundsCheck(t, start, end);
    t *= 2.f;
    if (t < 1.f) 
        return -end/2.f * (sqrtf(1.f - t * t) - 1.f) + start - 1.f;
    t -= 2.f;
    return end/2.f * (sqrtf(1.f - t * t) + 1.f) + start - 1.f;
}