Had to re-tile a large image, so spent a bit of time converting tile cutter to use NSOperationQueue. After a little playing, I opted for one operation per row, which seems to give the best all-around performance for the widest variety of images. You can download the latest version from here, or pull the source from GitHub.
For those of you having trouble running the application, I've also added i386 to the supported architectures. Because of my use of blocks, Snow Leopard is required to run the app.
Saturday, October 30, 2010
Friday, October 29, 2010
OpenGL ES 2.0 for iOS, Chapter 3 - Fundamentals of 3D Programming
Before we start writing code, we need to go over some of the basics concept and algorithms used in 3D programming. Essentially, we need to make sure we're all speaking the same language. In this chapter, we're going to discuss some of the most basic and fundamental concepts underlying the use of OpenGL ES 2.0, as well as some of the data structures and algorithms that we'll need to create and manipulate virtual three-dimensional objects. We'll talk about what vertices, vectors, polygons, and colors are and how they are represented in OpenGL ES.
We'll also look at some of the math that you'll need to perform on each of them. The math involved in computer graphics can be mind-numbingly complex at times, but don't worry, we're going to ease into the math slowly. I know it's a little bit of a challenge to dive into the math before we even create our first program, but what we're talking about in this chapter are the building blocks that will form the foundation of everything else we create. For many of you, much of this chapter will be a review of some pretty basic geometry, trigonometry, and linear algebra concepts you may have learned in college or high school, but don't get scared off if it's all completely new to you.
The Cartesian coordinate system defines an arbitrary point called the origin. This point is where the value of X, Y, and Z are all 0.0. Each of the three axes are like rulers with imaginary, evenly spaced numbers on them. If, for example, one object is to the right of another object, we assign it a higher X value than the other object. If it is above the other object, it has a higher Y value. By referencing the origin, any point in space can be described using a sequence of three numbers. A point where X is equal to +3, Y is equal to +1, and Z is equal to -1 is a little to the right, above, and behind the origin.
The Cartesian Coordinate System
When programming in OpenGL ES, the location of a single vertex is typically represented as an array of variables with a length of three: one to represent the X value, one to represent the Y value, and one to represent the Z value. Most often, we use an array of GLfloats for this purpose, but it doesn't have to be; OpenGL ES allows you to select the datatype you want by selecting the appropriate “alphabet soup” version of functions. Because of the design of the GPUs currently used on iOS devices, GLfloat is generally the best choice.
To allocate memory for a single vertex and assign its location value, you might do something like this:
The order of the values we use here is important. OpenGL ES always expects the vertex data to be submitted in a specific order: first X, then Y, and then Z.
More often than not, you'll be working with more than one vertex. You can't make very interesting models out of a single vertex. In fact, you're pretty much limited to making a dot. Take my word for it, being limited to drawing a dot isn't all that much fun. When you have to submit multiple vertices to OpenGL ES at the same time, OpenGL ES expects you to provide an array that's large enough to hold the data for all of the vertices. It also expects to receive the data in a specific order: first the X, Y, and Z value of the first vertex, then the X, Y, and Z value of the next vertex, and so on. For example, to allocate enough space for 9 vertices (which requires a total of 27 values) and assign values to them you might do something like this:
Once your data model consists of more than a handful of vertices, your code can get pretty unwieldy. Fortunately, most of the time your vertex data will come from external files generated by a 3D modeling program, rather than being done with long sequences of variable assignments like I'm showing here, but even so, trying to remember which axis and vertex a particular index in an array corresponds to is a pain. Quickly, now, what's the index for the Z axis of the 7th vertex? I know, right? More math! Sheesh.
We can save ourselves some grief and make our code much more readable by defining a struct to represent a single vertex like this:
A Vertex3D represents a single point in space. As far as what happens when you compile your code, allocating a single Vertex3D is exactly the same as allocating an array of three GLfloats, but now our code becomes easier to read:
This code is exactly the same as the earlier code as far as the compiler is concerned, but this code is much more readable. If we want to assign something to the Z axis of the seventh vertex, we just do this:²
Of course, in real programs, often the vertex data you'll be using will be too big to create effectively on the stack and will come, instead, from data files created in 3D modeling packages. Fortunately, creating space for vertices on the heap is just about as easy:
As you can see from the code sample, we can use vertices allocated on the heap just like we did earlier with the array of vertices allocated on the stack, thanks to the C language's pointer and array equivalency. The only difference between vertices on the heap and on the stack is that with heap allocated vertices, you need to remember to free your memory when you're done with it. We'll talk more about strategies for managing memory later in the book. For the first several exercises, we'll be using small numbers of vertices and will just be allocating them on the stack.
Even very complex shapes can be created using nothing but triangles
There are a few more things you need to know about triangles, however. In OpenGL ES, there is a concept known as winding, which just means the order in which the vertices are drawn matters. Unlike objects in the real world, polygons in OpenGL do not generally have two sides to them. They have one side, which is considered the frontface and, by default, a triangle can only be seen if its frontface if facing the viewer. While it is possible to configure OpenGL to treat polygons as two-sided, by default, triangles have only one visible side. By knowing which is the front or visible side of the polygon, OpenGL is able to do half the amount of calculations per polygon that it would have to do if both sides were treated as visible.
Although there are times when a polygon will stand on its own, and you might very well want the back side drawn, usually a triangle is part of a larger object, and one side of the polygon will be facing the inside of the object and thus will never be seen. The side that isn't drawn is called a backface, and OpenGL determines which is the front face to be drawn and which is the backface by looking at the drawing order of the vertices, which is the order they are submitted to OpenGL ES. By default, the front face is the one that would be drawn by following the vertices in counter-clockwise order. Since OpenGL can determine easily which triangles are visible to the user, it can use a process called backface culling to avoid doing work for polygons that aren't facing the viewer and, therefore, can't be seen.
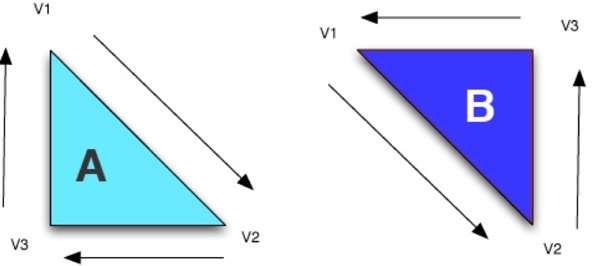
The Winding Rule
In the illustration above, the lighter triangle on the left marked “A” is a backface and won't be drawn because the order that the vertices would be drawn in relation to the viewer is clockwise. On the other hand, the darker triangle on the right labeled “B” is a frontface that will be drawn because the order of the vertices is counter-clockwise in relation to the viewer.
Here's the funny thing about vectors: they look almost exactly like vertices. They contain three values, one for each Cartesian axis. In code, they looks like this:
Yeah, that looks pretty much exactly like the Vector3D struct we created a moment ago, doesn't it? In fact, we could actually just use the same struct for both, by doing this:
So, what's going on here? Why do we have two different things that look exactly the same? How can a single point in space represent a direction and a distance? Well, a vector actually has two points in space. The one represented by the X, Y, and Z values, and the origin. Think of a vector as an imaginary line or arrow drawn from the origin to a specific point in space. The further a point is from the origin, the greater the velocity or distance it represents. With vectors, the distance from the origin to the stored position is known as the vector's magnitude.
Because the Vertex3D and Vector3D structures are exactly the same, a lot of 3D libraries and code do not bother defining two distinct datatypes. They just use the term “vector” generically to represent both vertices and vectors, or even more generically to refer to short sequences of floating point numbers. In fact, GLSL, the programming language used to write shaders (which we'll start looking at in the next chapter), does exactly that. It uses “vector” datatypes to represent pretty much anything that's a sequence (or one-dimensional array) of floating point values, such as vertices, vectors, and even colors. In our C and Objective-C code, however, we're going to separate out vertices and vectors to help reinforce the fact that there are two different (albeit related) concepts at play here.
We obviously don't have time to cover all of trigonometry before getting started, but it's worth taking a second just to remind you what the three most basic trigonometric functions represent, since we'll be using them quite a bit throughout the book and, in many cases, understanding that is the lynchpin in understanding why something works.
Given any angle, you can construct an imaginary right-triangle. Given a particular angle (the one marked ϴ (theta) in the next figure, we can take the two lines that make up the angle and add a third imaginary line that connects the other two and form a right angle (90° angle) with one of the other two sides. As long as we have two vectors with a common starting point, we can add a third line to get a right triangle. The side of this triangle that is opposite the angle we're discussing is called, imaginatively, the opposite. The side of the triangle that is at a 90° angle with the opposite is called the adjacent. The remaining side, which is always the longest side of a right triangle, is called the hypotenuse.
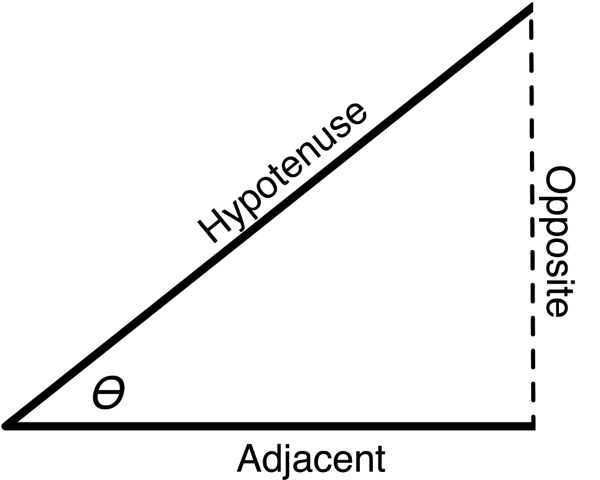
The Terminology of the Basic Trigonometric Functions
Now that we have some common terminology, let's look at the three basic functions:
When we use one of these operations in our code, I'll try to point out why we're using it, but it's not a bad idea to do a basic review of trigonometry if you're at all rusty. One important thing to remember about the C functions for sine, cosine, and tangent is that they expect and return angles represented as radians, not as degrees. Fortunately, it's relatively trivial to convert back and forth between radians and degrees by adding the following two macros to your code:
Once you have these macros, you can convert back and forth with ease. To convert a 45° angle to radians and then back to degrees, we can do this:
and see how I've drawn a triangle so that the line between the two vertices is the hypotenuse.
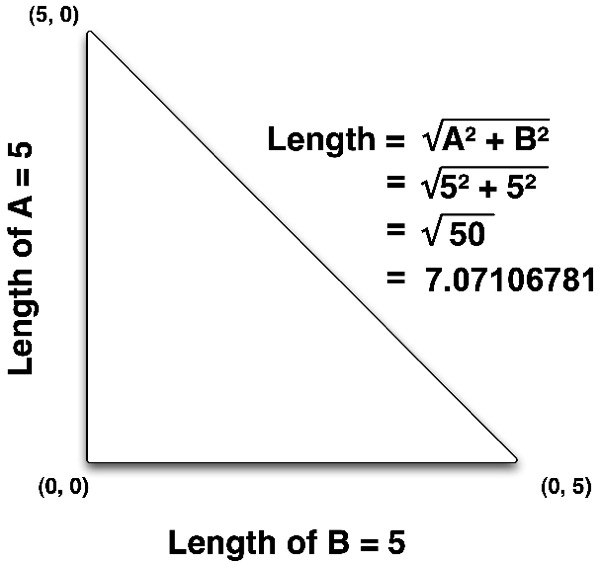
The Pythagorean Formula used to calculate distance between two-dimensional vertices
Since I've drawn a right triangle, the length of the other two sides of the triangle are pretty easy to calculate because it's basically the difference between the two vertices. If we subtract the X value of one vertex from the X value of the other vertex, that gives us one of the other two sides. If we do the same thing with the Y value, we get the distance of the other side and then we can calculate the hypotenuse using the Pythagorean Formula. In high school math, we learn that the Pythagorean Formula isA + B = C , so the distance of the hypotenuse can be calculated by squaring the other two sides, adding them together, and calculating the square root of the sum.
It turns out, however, that the calculation derived from Pythagoras's formula doesn't apply to just two dimensions: it works equally well when applied to three dimensions, or even when applied to larger coordinate systems. To calculate the distance between two three-dimensional vertices, we just calculate the difference between the X values and square it, then do the same with the Y and Z values, add them all together, and take the square root of the total.
Here's what it looks like in code:
Drawing two lines to represent two vectors
The origin of the name “cross product” is similar to that of the dot product. The same mathematician who discovered the dot product discovered the cross product calculation, and he used a cross symbol (×) to denote the operation in his writings, and the operation soon came to be known as the “cross product.”
Here's how you calculate the cross product of a vector:
Normalizing a Vector
For some purposes that vectors are used in graphics programming, the magnitude doesn't really matter. In some instances, the only information that's needed is the direction of the vector. In these situations, it's pretty common to do something called normalizing the vector. When you normalize a vector, you change its magnitude to 1.0 without changing the direction the vector points. The result of normalizing a vector is referred to as a unit vector or sometimes a normalized vector. The reason for normalizing vectors when the magnitude isn't used is that many calculations are shorter and faster when performed on unit vectors. In fact, normalizing one or more vectors is a step in many of the algorithms we'll use. If we normalize the vector once and store it that way, every subsequent operation performed can avoid normalizing it unless its value changes, since it's already been normalized.
Normalizing a vector is accomplished by dividing each of the three components (X, Y, Z) by the magnitude of the vector. The only gotcha is to make sure you don't divide by zero. Here's how you calculate it:
Very often, when you need to subtract vectors, you'll want the result to be expressed as a unit vector. Here's another function to calculate a unit vector based on two vertices, which leverages the previous function, then normalizes the result:
To specify color, you can call an OpenGL ES function designed for that purpose and pass the four component values that make up the color you want to set. For example, to set the current drawing color, you would call glColor4f() and pass in the four components. To set the current color to an opaque red, for example, you would do this:
This technique is somewhat limiting, as you'll see in the next chapter, because everything that gets drawn — until the next time glColor4f() is called — will get drawn in red. To do anything sophisticated with colors, you'll need the ability to specify colors on a per-vertex basis. When you do that, OpenGL ES expects the color data to be specified the same way as with vertices: using an array of variables. As with vertices, the order that you specify the values matters. OpenGL ES expects colors to be specified with four elements and expects those elements to be provided in the order: red, green, blue, then alpha, like so:
Just like with vertices, dealing with large arrays of color components can get tedious. Fortunately, we can make our code more readable the same way we did with vertices, by defining a new datatype to represent a single color:
Before we can start coding, though, we need to look at the architecture and basic use of OpenGL ES 2.0's programmable pipeline so that we know where to put our code.
1 - This coordinate system, which is called “y up” for obvious reasons, is the most commonly used and it's the one we'll use use with OpenGL ES. There is, however, an alternate coordinate system where the Z and Y axis are swapped called, the “z up” coordinate system. In this coordinate system, the Z axis moves up and down and the Y axis moves towards and away from the viewer. This alternate coordinate system is used in many CAD software packages, as well as a small number of other 3D software packages, most notably the open source program called Blender. You can convert from the Z up coordinate system to the Y up coordinate systems by simply rotating objects 90° on the X axis.
2 - I probably don't need to tell you this, but just in case you're confused, remember that C is a zero-indexed language, so the seventh vertex has an index value of 6.
3 - Okay, there are actually six trigonometric functions — plus each one has an inverse or quasi-inverse functions — but these three are the most basic and are the ones most often used in 3D programming.
We'll also look at some of the math that you'll need to perform on each of them. The math involved in computer graphics can be mind-numbingly complex at times, but don't worry, we're going to ease into the math slowly. I know it's a little bit of a challenge to dive into the math before we even create our first program, but what we're talking about in this chapter are the building blocks that will form the foundation of everything else we create. For many of you, much of this chapter will be a review of some pretty basic geometry, trigonometry, and linear algebra concepts you may have learned in college or high school, but don't get scared off if it's all completely new to you.
The Cartesian Coordinate System
The first thing you need to understand before doing any 3D graphics programming is how locations are represented in a three-dimensional world. In order to describe the position of any particular point in space, we use three imaginary lines that we call axes that are typically named X, Y, and Z. The X axis is an imaginary line that runs from left to right from the perspective of the viewer, the Y axis is an imaginary line that runs up and down, and the Z axis is an imaginary line that extends towards the viewer and away from him or her.¹OpenGL ES Units
One of the questions that may pop to mind when we talk about Cartesian coordinates is, "What units are we talking about here?" When we say that Y equals 1.383, what does that mean? It's 1.383 units from the origin, but what are those units?
Well, they're OpenGL units. They're completely arbitrary. When you design your program, you get to decide what they represent. Each unit could be a meter, a foot, and inch, or a fathom, whichever your application needs.
One of the questions that may pop to mind when we talk about Cartesian coordinates is, "What units are we talking about here?" When we say that Y equals 1.383, what does that mean? It's 1.383 units from the origin, but what are those units?
Well, they're OpenGL units. They're completely arbitrary. When you design your program, you get to decide what they represent. Each unit could be a meter, a foot, and inch, or a fathom, whichever your application needs.
The Cartesian coordinate system defines an arbitrary point called the origin. This point is where the value of X, Y, and Z are all 0.0. Each of the three axes are like rulers with imaginary, evenly spaced numbers on them. If, for example, one object is to the right of another object, we assign it a higher X value than the other object. If it is above the other object, it has a higher Y value. By referencing the origin, any point in space can be described using a sequence of three numbers. A point where X is equal to +3, Y is equal to +1, and Z is equal to -1 is a little to the right, above, and behind the origin.
Vertices
In order to define objects in a virtual 3D world, we use the three axes to define points in space and then connect them. To draw a triangle, for example, we would define three points in space, which means three X, three Y, and three Z values; the X, Y, and Z values have to be grouped together so we know which X goes with which Y and which Z. We call this grouping of a single X, Y, and Z value a vertex. A vertex represents a single point in space, and it is the atomic unit of three-dimensional graphics.When programming in OpenGL ES, the location of a single vertex is typically represented as an array of variables with a length of three: one to represent the X value, one to represent the Y value, and one to represent the Z value. Most often, we use an array of GLfloats for this purpose, but it doesn't have to be; OpenGL ES allows you to select the datatype you want by selecting the appropriate “alphabet soup” version of functions. Because of the design of the GPUs currently used on iOS devices, GLfloat is generally the best choice.
To allocate memory for a single vertex and assign its location value, you might do something like this:
GLfloat vertex[3];
vertex[0] = 12.234f; // X axis value
vertex[1] = -1.253f; // Y axis value
vertex[2] = 0.512f; // Z axis value
The order of the values we use here is important. OpenGL ES always expects the vertex data to be submitted in a specific order: first X, then Y, and then Z.
More often than not, you'll be working with more than one vertex. You can't make very interesting models out of a single vertex. In fact, you're pretty much limited to making a dot. Take my word for it, being limited to drawing a dot isn't all that much fun. When you have to submit multiple vertices to OpenGL ES at the same time, OpenGL ES expects you to provide an array that's large enough to hold the data for all of the vertices. It also expects to receive the data in a specific order: first the X, Y, and Z value of the first vertex, then the X, Y, and Z value of the next vertex, and so on. For example, to allocate enough space for 9 vertices (which requires a total of 27 values) and assign values to them you might do something like this:
GLfloat vertices[27];
vertex[0] = 12.234f; // X axis for first vertex
vertex[1] = -1.253f; // Y axis for first vertex
vertex[2] = 0.512f; // Z axis for first vertex
vertex[3] = -3.359f; // X axis for second vertex
vertex[4] = 52.03f; // Y axis for second vertex
vertex[5] = -18.23f; // Z axis for second vertex
// ... etc.
Once your data model consists of more than a handful of vertices, your code can get pretty unwieldy. Fortunately, most of the time your vertex data will come from external files generated by a 3D modeling program, rather than being done with long sequences of variable assignments like I'm showing here, but even so, trying to remember which axis and vertex a particular index in an array corresponds to is a pain. Quickly, now, what's the index for the Z axis of the 7th vertex? I know, right? More math! Sheesh.
We can save ourselves some grief and make our code much more readable by defining a struct to represent a single vertex like this:
typedef struct
{
GLfloat x;
GLfloat y;
GLfloat z;
} Vertex3D;
A Vertex3D represents a single point in space. As far as what happens when you compile your code, allocating a single Vertex3D is exactly the same as allocating an array of three GLfloats, but now our code becomes easier to read:
Vertex3D vertex;
vertex.x = 12.234f;
vertex.y = -1.253f;
vertex.z = 0.512f;
Wait… struct?
As you almost certainly know, the iOS SDK uses the Objective-C language, which is an object-oriented superset of the C language. So, you may be wondering why we've used an old-fashioned struct rather than defining an Objective-C object to represent vertices.
The answer is quite simply one of performance. Today's iPhones are capable of drawing objects comprised of hundreds of thousands or even millions of vertices every second. There are a couple of issues here. First, OpenGL ES is not an object-oriented library, and it expects to be given data in C arrays using raw datatypes. That means if we used objects to store each vertex, we'd have to be constantly unboxing the data from our objects into C arrays to hand the data off to OpenGL ES, which would incur processing overhead and slow our program down.
Additionally, there is extra overhead associated with Objective-C objects both in terms of memory allocation and message dispatching. This overhead is inconsequential in most parts of most applications, but when you're moving around hundreds of thousands of these things every second, that overhead can become non-trivial. As a result, it makes sense to store low-level data like vertices using native C data structures. We'll use Objective-C objects later in the book for higher level objects, of which we won't have quite so many.
As you almost certainly know, the iOS SDK uses the Objective-C language, which is an object-oriented superset of the C language. So, you may be wondering why we've used an old-fashioned struct rather than defining an Objective-C object to represent vertices.
The answer is quite simply one of performance. Today's iPhones are capable of drawing objects comprised of hundreds of thousands or even millions of vertices every second. There are a couple of issues here. First, OpenGL ES is not an object-oriented library, and it expects to be given data in C arrays using raw datatypes. That means if we used objects to store each vertex, we'd have to be constantly unboxing the data from our objects into C arrays to hand the data off to OpenGL ES, which would incur processing overhead and slow our program down.
Additionally, there is extra overhead associated with Objective-C objects both in terms of memory allocation and message dispatching. This overhead is inconsequential in most parts of most applications, but when you're moving around hundreds of thousands of these things every second, that overhead can become non-trivial. As a result, it makes sense to store low-level data like vertices using native C data structures. We'll use Objective-C objects later in the book for higher level objects, of which we won't have quite so many.
This code is exactly the same as the earlier code as far as the compiler is concerned, but this code is much more readable. If we want to assign something to the Z axis of the seventh vertex, we just do this:²
Vertex3D vertices[9];
vertex[6].z = newValue;
Of course, in real programs, often the vertex data you'll be using will be too big to create effectively on the stack and will come, instead, from data files created in 3D modeling packages. Fortunately, creating space for vertices on the heap is just about as easy:
Vertex3D *vertices = malloc(9 * sizeof(GLfloat));
vertices[0].x = 12.234f
vertices[0].y = -1.253f;
vertices[0].z = 0.512f;
As you can see from the code sample, we can use vertices allocated on the heap just like we did earlier with the array of vertices allocated on the stack, thanks to the C language's pointer and array equivalency. The only difference between vertices on the heap and on the stack is that with heap allocated vertices, you need to remember to free your memory when you're done with it. We'll talk more about strategies for managing memory later in the book. For the first several exercises, we'll be using small numbers of vertices and will just be allocating them on the stack.
Assembling Vertices: Polygons
Multiple vertices can be used to represent lots of little dots, such as stars or raindrops. But the real power of vertices is when you start putting them together to create shapes and solid objects. When you pass a bunch of vertices into OpenGL ES, you specify how it should draw them, a process we'll look at starting in the next chapter. The next building block up from the humble vertex is the polygon. As you probably remember from high school geometry, polygons are enclosed shapes that rest on a plane. The simplest polygon, and the only one that OpenGL ES allows us to use is the triangle, which, of course, has three sides. Having to use only triangles might sound like a bit of a limitation, but it's really not. Any polygon can be divided up into triangles and even very complex shapes can be represented using nothing but triangles. Also, the hardware inside the iPhone is very, very good and very fast at drawing triangles.
There are a few more things you need to know about triangles, however. In OpenGL ES, there is a concept known as winding, which just means the order in which the vertices are drawn matters. Unlike objects in the real world, polygons in OpenGL do not generally have two sides to them. They have one side, which is considered the frontface and, by default, a triangle can only be seen if its frontface if facing the viewer. While it is possible to configure OpenGL to treat polygons as two-sided, by default, triangles have only one visible side. By knowing which is the front or visible side of the polygon, OpenGL is able to do half the amount of calculations per polygon that it would have to do if both sides were treated as visible.
Although there are times when a polygon will stand on its own, and you might very well want the back side drawn, usually a triangle is part of a larger object, and one side of the polygon will be facing the inside of the object and thus will never be seen. The side that isn't drawn is called a backface, and OpenGL determines which is the front face to be drawn and which is the backface by looking at the drawing order of the vertices, which is the order they are submitted to OpenGL ES. By default, the front face is the one that would be drawn by following the vertices in counter-clockwise order. Since OpenGL can determine easily which triangles are visible to the user, it can use a process called backface culling to avoid doing work for polygons that aren't facing the viewer and, therefore, can't be seen.
In the illustration above, the lighter triangle on the left marked “A” is a backface and won't be drawn because the order that the vertices would be drawn in relation to the viewer is clockwise. On the other hand, the darker triangle on the right labeled “B” is a frontface that will be drawn because the order of the vertices is counter-clockwise in relation to the viewer.
Vectors
There's another piece of data that we'll be using a lot in 3D programming called a Euclidian vector, usually referred to as just a vector. A vector can represent both a direction and also a distance. Point your finger and extend your arm all the way so that you're pointing at something around you and your arm is straight. Your arm and finger are pretty much serving as a vector right now. One way vectors are used in 3D programming is when defining a directional light, like a spotlight. To define the direction that the light is pointing, we use a vector. If you were a virtual light, your finger might be the vector identifying what you were shining on.Here's the funny thing about vectors: they look almost exactly like vertices. They contain three values, one for each Cartesian axis. In code, they looks like this:
typedef struct
{
GLfloat x;
GLfloat y;
GLfloat z;
} Vector3D;
Yeah, that looks pretty much exactly like the Vector3D struct we created a moment ago, doesn't it? In fact, we could actually just use the same struct for both, by doing this:
typedef Vertex3D Vector3D;
Vector Components
A little later in the book, you'll see that vectors can have a fourth component called w. However, we'll rarely need to use the w value in our application code; it usually comes into play in code that runs in our shaders, so the datatypes we define here don't need the value.
A little later in the book, you'll see that vectors can have a fourth component called w. However, we'll rarely need to use the w value in our application code; it usually comes into play in code that runs in our shaders, so the datatypes we define here don't need the value.
So, what's going on here? Why do we have two different things that look exactly the same? How can a single point in space represent a direction and a distance? Well, a vector actually has two points in space. The one represented by the X, Y, and Z values, and the origin. Think of a vector as an imaginary line or arrow drawn from the origin to a specific point in space. The further a point is from the origin, the greater the velocity or distance it represents. With vectors, the distance from the origin to the stored position is known as the vector's magnitude.
Because the Vertex3D and Vector3D structures are exactly the same, a lot of 3D libraries and code do not bother defining two distinct datatypes. They just use the term “vector” generically to represent both vertices and vectors, or even more generically to refer to short sequences of floating point numbers. In fact, GLSL, the programming language used to write shaders (which we'll start looking at in the next chapter), does exactly that. It uses “vector” datatypes to represent pretty much anything that's a sequence (or one-dimensional array) of floating point values, such as vertices, vectors, and even colors. In our C and Objective-C code, however, we're going to separate out vertices and vectors to help reinforce the fact that there are two different (albeit related) concepts at play here.
Trigonometry Review
In lot of the math we'll be doing throughout this book, we're going to use the three basic trigonometric functions³. Trigonometry is nominally the study of right triangles, but it's also the computational component of geometry, and that's really what 3D graphics programming is: computational geometry combined with some linear algebra. That's a little bit of an oversimplification, but not completely untrue.We obviously don't have time to cover all of trigonometry before getting started, but it's worth taking a second just to remind you what the three most basic trigonometric functions represent, since we'll be using them quite a bit throughout the book and, in many cases, understanding that is the lynchpin in understanding why something works.
Given any angle, you can construct an imaginary right-triangle. Given a particular angle (the one marked ϴ (theta) in the next figure, we can take the two lines that make up the angle and add a third imaginary line that connects the other two and form a right angle (90° angle) with one of the other two sides. As long as we have two vectors with a common starting point, we can add a third line to get a right triangle. The side of this triangle that is opposite the angle we're discussing is called, imaginatively, the opposite. The side of the triangle that is at a 90° angle with the opposite is called the adjacent. The remaining side, which is always the longest side of a right triangle, is called the hypotenuse.
Now that we have some common terminology, let's look at the three basic functions:
| Function | C function | Definition |
|---|---|---|
| Sine | sinf() | The ratio of the length of the opposite to the length of the hypotenuse |
| Cosine | cosf() | The ratio of the length of the adjacent to the length of the hypotenuse |
| Tangent | tanf() | The ratio of the length of the opposite to the length of the adjacent |
When we use one of these operations in our code, I'll try to point out why we're using it, but it's not a bad idea to do a basic review of trigonometry if you're at all rusty. One important thing to remember about the C functions for sine, cosine, and tangent is that they expect and return angles represented as radians, not as degrees. Fortunately, it's relatively trivial to convert back and forth between radians and degrees by adding the following two macros to your code:
#define DEGREES_TO_RADIANS(x) ((x) / 180.0 * M_PI)
#define RADIANS_TO_DEGREES(x) ((x) / M_PI * 180.0)
Once you have these macros, you can convert back and forth with ease. To convert a 45° angle to radians and then back to degrees, we can do this:
GLfloat radians = DEGREES_TO_RADIANS(45);
GLfloat degrees = RADIANS_TO_DEGREES(radians); // will be 45
Basic Vector and Vertex Math
There are a number of different mathematical operations you will need to perform on vectors and vertices. Many of these are building blocks for more complex algorithms we'll be writing in future chapters, so it's important you understand all the functionality we're about to discuss. You don't necessarily need to fully understand the theoretical underpinnings of every function, however. This book focuses on practical applications and not as much on theory, so I'm not going to give you a mathematical proof for each formula and I'm going to express everything algorithmically in code, rather than using mathematical formulae.Calculating Distance Between Vertices
One thing you will likely need to calculate from time to time is the distance between two vertices. That is, if you were to draw a straight line between the two points, how long would that line be. Believe it or not, the calculation to do this is actually based on the Pythagorean formula. If we create a right triangle using the line from the first vertex to the second vertex as the hypotenuse, we can then use the Pythagorean formula to calculate the length of the distance between the two vertices. This is easier to visualize first in two dimensions, so look at
Since I've drawn a right triangle, the length of the other two sides of the triangle are pretty easy to calculate because it's basically the difference between the two vertices. If we subtract the X value of one vertex from the X value of the other vertex, that gives us one of the other two sides. If we do the same thing with the Y value, we get the distance of the other side and then we can calculate the hypotenuse using the Pythagorean Formula. In high school math, we learn that the Pythagorean Formula is
It turns out, however, that the calculation derived from Pythagoras's formula doesn't apply to just two dimensions: it works equally well when applied to three dimensions, or even when applied to larger coordinate systems. To calculate the distance between two three-dimensional vertices, we just calculate the difference between the X values and square it, then do the same with the Y and Z values, add them all together, and take the square root of the total.
Here's what it looks like in code:
static inline GLfloat Vertex3DDistanceBetweenVertices
(Vertex3D vertex1, Vertex3D vertex2)
{
GLfloat deltaX, deltaY, deltaZ;
deltaX = vertex2.x - vertex1.x;
deltaY = vertex2.y - vertex1.y;
deltaZ = vertex2.z - vertex1.z;
return sqrtf((deltaX * deltaX) +
(deltaY * deltaY) +
(deltaZ * deltaZ));
}
Inline Functions
You'll notice that I'm using the static and inline keywords for all of the fundamental math functions in this chapter. Inlining these functions eliminates the overhead of a function call. Essentially, at compile time, the code from the inline function gets copied into the function from which it was called. This is a trade-off, basically increasing the compiled size of the application slightly to eliminate the overhead of a function call. Because some of these functions may be called frequently, even thousands of times a second, it makes sense to inline them.
All of the code in this chapter and all the inline functions in the book will work as regular C functions. To use them that way, just remove the static inline keywords and place them in a .c or .m file instead of in a .h file, which is where inline methods are typically placed.
If you're a C++ programmer, you might be thinking that the static keyword is a bad idea. It's actually correct and a good idea in C and Objective-C programs, but it also true that it shouldn't be used if you're using C++ or Objective-C++. With C and Objective-C, the static keyword allows the compiler to remove the generated assembly for unused inline functions. However, with C++ or Objective-C++, the static keyword can potentially impact linkage behavior and offers no real benefit. So, if you're using either of those languages, consider removing the static keyword.
You'll notice that I'm using the static and inline keywords for all of the fundamental math functions in this chapter. Inlining these functions eliminates the overhead of a function call. Essentially, at compile time, the code from the inline function gets copied into the function from which it was called. This is a trade-off, basically increasing the compiled size of the application slightly to eliminate the overhead of a function call. Because some of these functions may be called frequently, even thousands of times a second, it makes sense to inline them.
All of the code in this chapter and all the inline functions in the book will work as regular C functions. To use them that way, just remove the static inline keywords and place them in a .c or .m file instead of in a .h file, which is where inline methods are typically placed.
If you're a C++ programmer, you might be thinking that the static keyword is a bad idea. It's actually correct and a good idea in C and Objective-C programs, but it also true that it shouldn't be used if you're using C++ or Objective-C++. With C and Objective-C, the static keyword allows the compiler to remove the generated assembly for unused inline functions. However, with C++ or Objective-C++, the static keyword can potentially impact linkage behavior and offers no real benefit. So, if you're using either of those languages, consider removing the static keyword.
Vector Magnitude
Earlier, I said that a vector could store both a direction and a distance or velocity. That information is referred to as the vector's magnitude and it's used in a number of places in 3D programming. We can extract that information by using the Vertex3DDistanceBetweenVertices() function we just wrote, passing the origin as vertex1 and the vector as vertex2. However, there's no point in doing a delta between a vector and the origin. Remember, the origin is at {0,0,0} and the difference between any number and 0 is itself, so we end up doing unnecessary calculations if we do that. Therefore, for calculating the magnitude of a vector, we can simplify the distance formula above by removing the delta operation, like so:static inline GLfloat Vector3DMagnitude(Vector3D vector)
{
return sqrtf((vector.x * vector.x) +
(vector.y * vector.y) +
(vector.z * vector.z));
}
The f is Important!
Notice that I've used sqrtf() instead of sqrt(). Most of the basic C math functions provided in <math.h> expect double-precision floating point variables as arguments and return double-precision floating point values. But OpenGL ES doesn't support double-precision floating point values. That means if you use sqrt() or any of the other functions that don't end in f, you're potentially making your code do calculations on twice the precision you need, plus you might be forcing your application to do runtime conversion from float to double and back.
Notice that I've used sqrtf() instead of sqrt(). Most of the basic C math functions provided in <math.h> expect double-precision floating point variables as arguments and return double-precision floating point values. But OpenGL ES doesn't support double-precision floating point values. That means if you use sqrt() or any of the other functions that don't end in f, you're potentially making your code do calculations on twice the precision you need, plus you might be forcing your application to do runtime conversion from float to double and back.
Vector Dot Product
Next up on our tour of vector math is something called the vector dot product (also sometimes called the scalar product). The dot product can be used to calculate the angle between two vectors because the value returned by the dot product for two unit vectors happens to equal the cosine of the angle between the vectors. As a result, the dot product is a building block function that is used for a lot of purposes in 3D programming. The actual calculation is relatively simple. You multiply the X values of the two vectors, the Y values of the two vectors, and the Z values of the two vectors, then add those three products together. The name “dot product” doesn't have any real significance; it originates from the fact that the operation was represented by a dot (•) in the notes of Joseph Louis Lagrange, the mathematician who discovered it, a usage that has since passed into use in mathematical notation. Here is what the vector dot product looks like in code:static inline GLfloat Vector3DDotProduct
(Vector3D vector1, Vector3D vector2)
{
return (vector1.x*vector2.x) +
(vector1.y*vector2.y) +
(vector1.z*vector2.z);
}
Vector Cross Product
There's another “building block” function that you'll need to know called the cross product. The result of a cross product calculation on two vectors is another vector that is perpendicular to both of the original vectors. To visualize this, take a piece of paper and draw a line on it to represent one vector. Now, draw a second line starting at the same point as the first one, but going in a different direction, similar to what you see in the next illustration. The cross product of these two vectors would be a line sticking straight out of the paper at a 90° angle. If you take a pencil and put it down on the paper so the eraser is on the point where the two lines meet, you have a pretty good representation of the result of the cross product calculation with those two vectors.
The origin of the name “cross product” is similar to that of the dot product. The same mathematician who discovered the dot product discovered the cross product calculation, and he used a cross symbol (×) to denote the operation in his writings, and the operation soon came to be known as the “cross product.”
Here's how you calculate the cross product of a vector:
static inline Vector3D Vector3DCrossProduct(Vector3D vector1, Vector3D vector2)
{
Vector3D ret;
ret.x = (vector1.y * vector2.z) - (vector1.z * vector2.y);
ret.y = (vector1.z * vector2.x) - (vector1.x * vector2.z);
ret.z = (vector1.x * vector2.y) - (vector1.y * vector2.x);
return ret;
}
Normalizing a Vector
For some purposes that vectors are used in graphics programming, the magnitude doesn't really matter. In some instances, the only information that's needed is the direction of the vector. In these situations, it's pretty common to do something called normalizing the vector. When you normalize a vector, you change its magnitude to 1.0 without changing the direction the vector points. The result of normalizing a vector is referred to as a unit vector or sometimes a normalized vector. The reason for normalizing vectors when the magnitude isn't used is that many calculations are shorter and faster when performed on unit vectors. In fact, normalizing one or more vectors is a step in many of the algorithms we'll use. If we normalize the vector once and store it that way, every subsequent operation performed can avoid normalizing it unless its value changes, since it's already been normalized.
Normalizing a vector is accomplished by dividing each of the three components (X, Y, Z) by the magnitude of the vector. The only gotcha is to make sure you don't divide by zero. Here's how you calculate it:
static inline void Vector3DNormalize(Vector3D *vector)
{
GLfloat vecMag = Vector3DMagnitude(*vector);
if ( vecMag == 0.0 )
{
vector->x = 1.0;
vector->y = 0.0;
vector->z = 0.0;
return;
}
vector->x /= vecMag;
vector->y /= vecMag;
vector->z /= vecMag;
}
Creating a Vector from Two Vertices
Since a vector is basically just an imaginary line between two vertices, any time that you have two vertices, you also have a vector. The line from one vertex to the other has a direction and a distance (or magnitude) just like a line from the origin to a vertex. As a result, you can create a single vector representing the angle and distance between two vertices by just subtracting the destination vertex from the source vertex. This can come in handy, for example, when working with lights. If you want to point a spotlight at a specific object, you can subtract the object's position from the light's position and the result will be a vector that points the light at the object. Subtracting vectors is simply subtracting each of the component values. You subtract the X value of one from the X value of the other, the Y value of one from the Y value of the other, the Z value of one from the Z value of the other, and you stick the results into a new Vector3D.static inline Vector3D Vector3DMakeWithStartAndEndPoints
(Vertex3D start, Vertex3D end)
{
Vector3D ret;
ret.x = end.x - start.x;
ret.y = end.y - start.y;
ret.z = end.z - start.z;
return ret;
}
Very often, when you need to subtract vectors, you'll want the result to be expressed as a unit vector. Here's another function to calculate a unit vector based on two vertices, which leverages the previous function, then normalizes the result:
static inline Vector3D Vector3DMakeNormalizedVectorWithStartAndEndPoints
(Vertex3D start, Vertex3D end)
{
Vector3D ret = Vector3DMakeWithStartAndEndPoints(start, end);
Vector3DNormalize(&ret);
return ret;
}
Flipping a Vector
There's one last operation we'll look at for vectors, and that's called flipping a vector. Flipping a vector is nothing more than making it point in exactly the opposite direction from where it currently points, without changing its magnitude. To flip a vector, you simply set each component (x,y,z) to negative the current value; so an X value of 5.5 becomes an X value of -5.5.static inline void Vector3DFlip (Vector3D *vector)
{
vector->x = -vector->x;
vector->y = -vector->y;
vector->z = -vector->z;
}
Colors
We're mostly done with math for this chapter, but before we can proceed to creating our first OpenGL ES 2.0 project, we should talk about one more fundamental datatype: color. The most commonly used computer representation of color involves the use of three or four numbers, which are the relative amounts of red, green, and blue light that make up the color. The fourth component, called alpha, isn't technically a component of the color but rather identifies how much of what's behind shows through. A color with an alpha value of 1.0 is completely opaque and is unaffected by anything drawn behind it. A color with an alpha value of 0.0 is completely transparent.To specify color, you can call an OpenGL ES function designed for that purpose and pass the four component values that make up the color you want to set. For example, to set the current drawing color, you would call glColor4f() and pass in the four components. To set the current color to an opaque red, for example, you would do this:
glColor4f (1.0f, 0.0f, 0.0f, 1.0f);
This technique is somewhat limiting, as you'll see in the next chapter, because everything that gets drawn — until the next time glColor4f() is called — will get drawn in red. To do anything sophisticated with colors, you'll need the ability to specify colors on a per-vertex basis. When you do that, OpenGL ES expects the color data to be specified the same way as with vertices: using an array of variables. As with vertices, the order that you specify the values matters. OpenGL ES expects colors to be specified with four elements and expects those elements to be provided in the order: red, green, blue, then alpha, like so:
GLfloat color[4];
color[0] = 1.f; // red
color[1] = 0.f; // green
color[2] = 0.f; // blue
color[3] = 1.f; // alpha
Just like with vertices, dealing with large arrays of color components can get tedious. Fortunately, we can make our code more readable the same way we did with vertices, by defining a new datatype to represent a single color:
typedef struct {
GLfloat red;
GLfloat green;
GLfloat blue;
GLfloat alpha;
} Color;
On To the Pipeline
Well, now you've seen the the most basic building blocks of three dimensional graphics: vertices, vectors, polygons, and colors. You've also had your head beat in with a little bit of vector math. I don't know about you, but that's about all the theory and math I can stand in one chunk. Don't worry, there's plenty more math to come, but let's see if we can't have some fun before we dive back into it. We can already do some graphics programming just with the math we know so far, so let's do it.Before we can start coding, though, we need to look at the architecture and basic use of OpenGL ES 2.0's programmable pipeline so that we know where to put our code.
1 - This coordinate system, which is called “y up” for obvious reasons, is the most commonly used and it's the one we'll use use with OpenGL ES. There is, however, an alternate coordinate system where the Z and Y axis are swapped called, the “z up” coordinate system. In this coordinate system, the Z axis moves up and down and the Y axis moves towards and away from the viewer. This alternate coordinate system is used in many CAD software packages, as well as a small number of other 3D software packages, most notably the open source program called Blender. You can convert from the Z up coordinate system to the Y up coordinate systems by simply rotating objects 90° on the X axis.
2 - I probably don't need to tell you this, but just in case you're confused, remember that C is a zero-indexed language, so the seventh vertex has an index value of 6.
3 - Okay, there are actually six trigonometric functions — plus each one has an inverse or quasi-inverse functions — but these three are the most basic and are the ones most often used in 3D programming.
Fabulapps Releases a Never-Ending Puzzle Game for the iPhone
The concept of this casual game is to find 15 lost pieces of the “last totem", and for this players have to solve levels through three different and beautiful worlds. Built around the very likable Kiko, who was in charge of guarding the last totem of the gods before it was stolen by Yaru, the Lord of the forbidden mountain.
The game features cool sound effects is optimized for the new iPhone 4 Retina Display and is easy to learn.
The new game from Fabulapps will be available through Apple’s App Store on October 28.
For more information click here
Thursday, October 28, 2010
OpenGL ES 2.0 for iOS Chapter 2 - Meet OpenGL ES
Before we actually start working with OpenGLS, let's take a few minutes to talk about its history. The evolution of OpenGL has greatly affected the architecture and the design of the library. As a result, it's worth investing a few minutes to understand where it comes from; it will help you to use it better. If you've primarily or only worked in object-oriented programming languages like Objective-C and Java, OpenGL ES can seem a little strange and even old-fashioned since it is a procedural API, not an object-oriented one.
It wasn't just the hardware that was different back then. The state of computer programming was also very different. Although the concept of object-oriented programming existed, it wasn't in mainstream use yet, and most computers were programmed using procedural languages like C, Pascal, and BASIC, or else were written directly in assembly language. As a result, IRIS GL was a library of procedural function calls that could be used from those languages, with C being the most common.
The Open Gamble
A decade from its inception, SGI had established itself as the industry leader for sophisticated graphics programming. In 1992, SGI decided to do a massive overhaul and re-write of IRIS GL, and they also decided to do something rather extraordinary: allow their competitors to license the new version of their graphics library. Even more extraordinary was the fact that they published the specification for their library as an open standard that anyone could implement. As a result, the revised graphics library could be ported to other hardware and software platforms, and graphic hardware vendors could make their products compatible with this new graphic language just by writing device drivers to the open standard. The rewrite of IRIS GL and the new open specification were both dubbed OpenGL. To this day, OpenGL is the only truly cross-platform, language-agnostic, hardware accelerated graphics library in common use. Its primary competitor, DirectX, is only available on Microsoft's operating systems, including the various Windows and Windows Mobile operating systems, as well as the OS that runs the Xbox and XBox 360.
OpenGL prospered. It began to be used not just for 3D-modeling programs and scientific simulations, but as computers got more powerful, it began to be used for 3D games. SGI didn't do quite as well as the library it created. As computers became more capable, the need for expensive high-end workstations like the ones SGI manufactured began to dwindle, and SGI became a shadow of its former self, eventually declaring bankruptcy a few years ago. Although there is a company today called Silicon Graphics, it is not the same company that once dominated the graphic programming industry; SGI sold its name to another company as part of their bankruptcy proceedings.
However, the same increase in computing power that contributed to SGI's downfall was a boon for cross-platform OpenGL. Before long, hardware accelerated graphics were being used everywhere. Since OpenGL allows programmers targeting any operating system to take advantage of hardware acceleration without having to write to any specific hardware, a program written using OpenGL could get the benefit of hardware acceleration regardless of the operating system, graphic card, or processor that it was run on (assuming, of course, that the graphic card supports OpenGL). This took a lot of the stress and work out of graphics programming because it meant that programmers no longer had to write to specific hardware in order to get good performance; they could just write to the standard. Code that writes directly to hardware tends to break on hardware it wasn't written for, so games written using OpenGL tend to be less fragile than those written directly to hardware and have longer shelf-lives. Programs written using OpenGL are also far easier to port to other computing platforms because the datatypes and function calls are exactly the same no matter where your code runs. OpenGL allows developers to spend less time on performance optimization and more time on the specific coding tasks needed by their application.
immediate mode (sometimes called direct mode, a slower, more tedious method of graphics programming that is mostly obsolete, but is still often used to teach graphics programming), double-precision floating point variables, and support for polygons other than triangles, to name just a few things. This new, leaner, more efficient graphic library was dubbed OpenGL for Embedded Systems, or just OpenGL ES.
One of the challenges facing the designers of OpenGL ES is that not all languages define exactly the same datatypes, and in some languages, like C, the exact size of those datatypes can vary. For example, the int datatype in C is based on the register size of the hardware being compiled for. That means an int can be compiled down to a different number of bytes on different hardware. To deal with this problem, OpenGL defines its own datatypes, all of which begin with the letters GL. When working in OpenGL ES, instead of using int, for example, you would probably choose to use GLint or maybe GLshort. While these are all integer datatypes and all work, the size of int is different on different platforms. The size of GLint and GLshort, however, are the same on every operating system, in every language, and on all hardware, giving more predictable results, avoiding runtime conversion, and generally making life much easier.
You should endeavor to use the OpenGL ES datatypes for any data that could potentially be submitted as part of an OpenGL ES library call, or that is retrieved from an OpenGL ES library call. For variables that will never interact with OpenGL, you do not have to use an OpenGL datatype and, in fact, you may find it makes your code clearer if you use the OpenGL datatypes only for values that will be used by OpenGL ES and use regular C datatypes like int or CoreFoundation datatypes like NSInteger everywhere else.
The OpenGL ES datatypes are as follows:
Always make an effort to use the smallest datatype that suits your needs. For example, if you know you will never have more than a thousand vertices in a particular object, don't use a GLint to store the vertex indices for that object, since a GLshort is more than capable of holding all the numbers up to a thousand. There are some exceptions to this rule that we'll talk about later in the book, but it's a good general rule to keep in mind while you're programming. Remember, the iPhone has limited memory resources compared to your laptop or desktop computer, and those extra bytes can add up.
A few things to notice when looking at the table above: first, there is no GLdouble. OpenGL ES 2.0 doesn't have double-precision floating point variables. These were intentionally left out due to OpenGL ES's emphasis on performance and resource utilization. The authors of the OpenGL ES specification felt that the screen sizes of embedded devices would not benefit from the use of double-precision (64-bit) floating point values, and that their use could very quickly eat up the limited system resources available on a these device. Second, the last two datatypes on the list, GLfixed and GLclampx, are used to represent floating point values using integer datatypes using something calledfixed point representation .
This is a common optimization on systems where floating point math performance is considerably slower than integer math performance. Since all iPhones, iPod touches, and the iPad have GPUs that work natively with floating point numbers and are capable of doing very fast floating point operations, we won't be discussing the use of fixed point mathematics in this book at all.
In OpenGL ES, this is not the case at all. Keeping with OpenGL ES's focus on performance, new versions of OpenGL ES often drop support for features used in the previous version, especially if a faster or more efficient way of accomplishing that task has been added to the later version. In order to take full advantage of today's iOS hardware, you have to use OpenGL ES 2.0. Even though current devices do support OpenGL ES 1.1, you can't intermix 1.1 and 2.0 code. As a result, this book deals exclusively with OpenGL ES 2.0.
glEnum error = glGetError();
This function is used to find out if any errors occurred in the previous OpenGL ES function call. Most OpenGL ES functions do not return an error code themselves, so you have to call this function separately if you want to find out if everything worked okay.
If a function does take one or more arguments, but it always and only takes one specific type of argument, then the function also generally will not have have characters at the end, such as:
glUseProgram(program);
In the Beginning, There Was IRIS GL
In 1981, a company called Silicon Graphics, Inc. (often referred to by their initials, SGI) was founded and started making high-end 3D graphic workstations. All of the early models of SGI machines were given the name “IRIS” along with a model number. IRIS was actually an acronym that stood for Integrated Raster Imaging System; of course, the acronym had a dual meaning, since “iris” is also an anatomical term referring to part of the eye. Graphics programming on these workstations was done using a set of APIs called the IRIS Graphics Language, usually shortened to IRIS GL. Now, if you were programming in the early 1980s, you probably remember that things were very different. Even if you weren't programming back then, you likely realize just how long 30 years is in the fast-moving technology industry. In 1981, the Mac hadn't been introduced yet. Consumer-level computers were machines like the Apple //e, the IBM PC, and the Commodore 64, none of which had the horsepower to effectively work with 3D graphics in real time. Most computers didn't have floating point processors, and dedicated graphics processors were extremely rare; they wouldn't become common for nearly another decade. The IRIS workstations, on the other hand, used much more sophisticated hardware than these consumer machines and were specifically designed to handle the large number of floating point calculations needed in 3D graphics programming.It wasn't just the hardware that was different back then. The state of computer programming was also very different. Although the concept of object-oriented programming existed, it wasn't in mainstream use yet, and most computers were programmed using procedural languages like C, Pascal, and BASIC, or else were written directly in assembly language. As a result, IRIS GL was a library of procedural function calls that could be used from those languages, with C being the most common.
What's in a Name?
IRIS GL is always written with a space between IRIS and GL and IRIS is always written in capital letters, because it's an acronym. On the other hand, OpenGL is written without any space between Open and GL and only the O, G, and L are capitalized.
IRIS GL is always written with a space between IRIS and GL and IRIS is always written in capital letters, because it's an acronym. On the other hand, OpenGL is written without any space between Open and GL and only the O, G, and L are capitalized.
The Open Gamble
A decade from its inception, SGI had established itself as the industry leader for sophisticated graphics programming. In 1992, SGI decided to do a massive overhaul and re-write of IRIS GL, and they also decided to do something rather extraordinary: allow their competitors to license the new version of their graphics library. Even more extraordinary was the fact that they published the specification for their library as an open standard that anyone could implement. As a result, the revised graphics library could be ported to other hardware and software platforms, and graphic hardware vendors could make their products compatible with this new graphic language just by writing device drivers to the open standard. The rewrite of IRIS GL and the new open specification were both dubbed OpenGL. To this day, OpenGL is the only truly cross-platform, language-agnostic, hardware accelerated graphics library in common use. Its primary competitor, DirectX, is only available on Microsoft's operating systems, including the various Windows and Windows Mobile operating systems, as well as the OS that runs the Xbox and XBox 360.
OpenGL prospered. It began to be used not just for 3D-modeling programs and scientific simulations, but as computers got more powerful, it began to be used for 3D games. SGI didn't do quite as well as the library it created. As computers became more capable, the need for expensive high-end workstations like the ones SGI manufactured began to dwindle, and SGI became a shadow of its former self, eventually declaring bankruptcy a few years ago. Although there is a company today called Silicon Graphics, it is not the same company that once dominated the graphic programming industry; SGI sold its name to another company as part of their bankruptcy proceedings.
The SGI Campus
At the height of success, SGI's headquarters were located in a beautiful multi-building complex in Mountain View, California,complete with swimming pool, forested walking trails, and 500,000 square feet of office space. The campus still exists today. Google uses it as their world headquarters and calls it the Googleplex.
At the height of success, SGI's headquarters were located in a beautiful multi-building complex in Mountain View, California,
However, the same increase in computing power that contributed to SGI's downfall was a boon for cross-platform OpenGL. Before long, hardware accelerated graphics were being used everywhere. Since OpenGL allows programmers targeting any operating system to take advantage of hardware acceleration without having to write to any specific hardware, a program written using OpenGL could get the benefit of hardware acceleration regardless of the operating system, graphic card, or processor that it was run on (assuming, of course, that the graphic card supports OpenGL). This took a lot of the stress and work out of graphics programming because it meant that programmers no longer had to write to specific hardware in order to get good performance; they could just write to the standard. Code that writes directly to hardware tends to break on hardware it wasn't written for, so games written using OpenGL tend to be less fragile than those written directly to hardware and have longer shelf-lives. Programs written using OpenGL are also far easier to port to other computing platforms because the datatypes and function calls are exactly the same no matter where your code runs. OpenGL allows developers to spend less time on performance optimization and more time on the specific coding tasks needed by their application.
The Rise of OpenGL ES
By 2006, it became apparent that the increases in computing power would soon lead to small, handheld devices capable of displaying 3D graphics. With an eye towards efficiency, a new graphics library was created by taking an older version of the OpenGL specification and stripping out some of the functionality that might have had a negative impact on performance. The team working on this new mobile graphics specification removedOpenGL Basics
Because they had a very complex procedural library, SGI realized early on that they had to come up with some very distinct and consistent naming patterns to make their library usable and developer-friendly. Understanding the naming conventions used by the designers of OpenGL makes it easier to find what you're looking for and makes it easier to understand what existing code is doing. When you first look at OpenGL code, it can look like a jumble of nonsense. Once you understand its naming conventions, however, the odd names start to make an awful lot of sense. Let's let's look at these conventions quickly before we go any further.One of the challenges facing the designers of OpenGL ES is that not all languages define exactly the same datatypes, and in some languages, like C, the exact size of those datatypes can vary. For example, the int datatype in C is based on the register size of the hardware being compiled for. That means an int can be compiled down to a different number of bytes on different hardware. To deal with this problem, OpenGL defines its own datatypes, all of which begin with the letters GL. When working in OpenGL ES, instead of using int, for example, you would probably choose to use GLint or maybe GLshort. While these are all integer datatypes and all work, the size of int is different on different platforms. The size of GLint and GLshort, however, are the same on every operating system, in every language, and on all hardware, giving more predictable results, avoiding runtime conversion, and generally making life much easier.
You should endeavor to use the OpenGL ES datatypes for any data that could potentially be submitted as part of an OpenGL ES library call, or that is retrieved from an OpenGL ES library call. For variables that will never interact with OpenGL, you do not have to use an OpenGL datatype and, in fact, you may find it makes your code clearer if you use the OpenGL datatypes only for values that will be used by OpenGL ES and use regular C datatypes like int or CoreFoundation datatypes like NSInteger everywhere else.
The OpenGL ES datatypes are as follows:
| Type | Bytes | Min | Max | Comment |
|---|---|---|---|---|
| GLenum | 4 | 0 | 4,294,967,295 | For enumerated types |
| GLboolean | 1 | 0 | 255 | Boolean value, GL_TRUE or GL_FALSE |
| GLbitfield | 4 | - | - | Holds up to 32 Booleans, one per bit |
| GLbyte | 1 | -128 | 127 | |
| GLshort | 2 | -32,768 | 32,767 | |
| GLint | 4 | -2,147,483,648 | 2,147,483,647 | |
| GLsizei | 4 | -2,147,483,648 | 2,147,483,647 | Similar to size_t |
| GLubyte | 1 | 0 | 255 | |
| GLushort | 2 | 0 | 65,535 | |
| GLuint | 4 | 0 | 4,294,967,295 | |
| GLfloat | 4 | - | - | Floating point variable |
| GLclampf | 4 | - | - | Floating point between 0.0 and 1.0 |
| GLvoid | - | - | - | No value |
| GLfixed | 4 | - | - | Fixed point numbers |
| GLclampx | 4 | - | - | Fixed-point between 0.0 and 1.0 |
Always make an effort to use the smallest datatype that suits your needs. For example, if you know you will never have more than a thousand vertices in a particular object, don't use a GLint to store the vertex indices for that object, since a GLshort is more than capable of holding all the numbers up to a thousand. There are some exceptions to this rule that we'll talk about later in the book, but it's a good general rule to keep in mind while you're programming. Remember, the iPhone has limited memory resources compared to your laptop or desktop computer, and those extra bytes can add up.
A few things to notice when looking at the table above: first, there is no GLdouble. OpenGL ES 2.0 doesn't have double-precision floating point variables. These were intentionally left out due to OpenGL ES's emphasis on performance and resource utilization. The authors of the OpenGL ES specification felt that the screen sizes of embedded devices would not benefit from the use of double-precision (64-bit) floating point values, and that their use could very quickly eat up the limited system resources available on a these device. Second, the last two datatypes on the list, GLfixed and GLclampx, are used to represent floating point values using integer datatypes using something called
This is a common optimization on systems where floating point math performance is considerably slower than integer math performance. Since all iPhones, iPod touches, and the iPad have GPUs that work natively with floating point numbers and are capable of doing very fast floating point operations, we won't be discussing the use of fixed point mathematics in this book at all.
OpenGL Versions
Both OpenGL and OpenGL ES come in several different versions. With workstation OpenGL, each newly released version tends to build on the old, but have historically remained almost completely backward-compatible with earlier versions. So, for example, most OpenGL 1.5 code will compile and run just fine using OpenGL 3.0. Versions 3.1, 3.2, and 4.0 have begun to remove Direct mode and a few other legacy features, but still maintain an incredible amount of backward compatibility with previous versions.In OpenGL ES, this is not the case at all. Keeping with OpenGL ES's focus on performance, new versions of OpenGL ES often drop support for features used in the previous version, especially if a faster or more efficient way of accomplishing that task has been added to the later version. In order to take full advantage of today's iOS hardware, you have to use OpenGL ES 2.0. Even though current devices do support OpenGL ES 1.1, you can't intermix 1.1 and 2.0 code. As a result, this book deals exclusively with OpenGL ES 2.0.
Alphabet Soup: OpenGL Functions
Because you're working with a procedural library, everything you do in OpenGL ES is accomplished by making standard C function calls, and all OpenGL ES functions begin with the letters gl. Many OpenGL ES functions also have a string of characters at the end that tell you a little bit about the parameters the function expects you to pass in. OpenGL ES functions that don't take any parameters don't have these letters at the end, for example:glEnum error = glGetError();
This function is used to find out if any errors occurred in the previous OpenGL ES function call. Most OpenGL ES functions do not return an error code themselves, so you have to call this function separately if you want to find out if everything worked okay.
If a function does take one or more arguments, but it always and only takes one specific type of argument, then the function also generally will not have have characters at the end, such as:
glUseProgram(program);
The function above, glUseProgram(), always and only takes a GLuint, and there are no other versions of this particular function. As a result, there's no alphabet soup at the end of the function name because there's no need for it. You have no choice in the datatype to pass in. Don't worry too much about what this function actually does for now; you'll start using it in a few chapters and will be very well acquainted with it by the end of the book.
Name by Any Other Name.
OpenGL has some terminology that can be downright confusing at times. OpenGL often takes words and gives them a very specific meaning that's different from ordinary English usage. Sometimes that usage is so different that the use of the term seems at odds with the plain-English meaning of the word. One example of this is the word name. In OpenGL parlance, a name is a number, usually a GLint or GLuint. In OpenGL ES, names are never a string and never have any semantic meaning. What OpenGL means by name is simply a unique identifier for a specific object. The reason for this is that integers are far more efficient to use to uniquely identify an object; strings comparisons, on the other hand, are costly.
When you ask OpenGL to create an object¹ for you using a function, it will assign a unique integer value to identify the object it creates and it will return that unique integer to the calling code. When you later want to do something with a specific object, you pass the object's name (the number returned by the earlier call) to OpenGL as one of the arguments to the function call in order to tell OpenGL ES which object the function call should act upon.
A great many OpenGL function calls can be made using more than one datatype, however. OpenGL ES gives you this flexibility so you can choose the most efficient data type for your needs. For these functions, The first and sometimes the second letter after the name of the function specify the datatype that this function expects. Here's what each suffix refers to:
So a function called glFoof() is glFoo that expects a GLfloat to be passed in as an argument, while glFoos() is the same function, but expects a GLshort. Since the name of the two functions is identical except for the letters at the end, you know that both function calls accomplish exactly the same task.
Sometimes, there is also a number as part of the function suffix. This number represents the number of values that the function expects. So, for example, the function glFoo1f() would expect a single GLfloats, while glFoo2f() would expect two GLfloats. Both methods would accomplish exactly the same task, however.
Some OpenGL ES functions serve a very generic purpose and need to be able to take a variable number of arguments or else need you to pass a value by reference so the function can change the original value. All OpenGL ES functions we've seen so far expect a single value per argument and those values are passed by value. This means the called function gets its own copy of each value, the number of arguments cannot change, and any changes made to those values by the called method do not impact the calling code. When OpenGL needs you to pass a pointer in as an argument, either because it needs to be able to change the value, or because it wants you to be able to pass in an indefinite number of arguments, it will add a v suffix at the end of the alphabet soup. For example, the function glFoo1fv() would expect you to pass in a single pointer to a GLfloat.
1 - Intermixing a functional library with an object-oriented language can sometimes lead to confusions. OpenGL ES has things it calls "objects", but they are not object as far as Objective-C is concerned. Usually, which type of object I'm referring to will be clear from the context, but when it's not, I'll try to identify whether “object” refers to an Objective-C object or an OpenGL object.
| Letter(s) | Datatype Taken |
|---|---|
| b | GLbyte |
| s | GLshort |
| i | GLint |
| f | GLfloat |
| ub | GLubyte |
| us | GLushort |
| ui | GLuint |
So a function called glFoof() is glFoo that expects a GLfloat to be passed in as an argument, while glFoos() is the same function, but expects a GLshort. Since the name of the two functions is identical except for the letters at the end, you know that both function calls accomplish exactly the same task.
Sometimes, there is also a number as part of the function suffix. This number represents the number of values that the function expects. So, for example, the function glFoo1f() would expect a single GLfloats, while glFoo2f() would expect two GLfloats. Both methods would accomplish exactly the same task, however.
Some OpenGL ES functions serve a very generic purpose and need to be able to take a variable number of arguments or else need you to pass a value by reference so the function can change the original value. All OpenGL ES functions we've seen so far expect a single value per argument and those values are passed by value. This means the called function gets its own copy of each value, the number of arguments cannot change, and any changes made to those values by the called method do not impact the calling code. When OpenGL needs you to pass a pointer in as an argument, either because it needs to be able to change the value, or because it wants you to be able to pass in an indefinite number of arguments, it will add a v suffix at the end of the alphabet soup. For example, the function glFoo1fv() would expect you to pass in a single pointer to a GLfloat.
Let's Begin
At this point, you should have a basic understanding of the where OpenGL ES came from and why it was designed the way it was. The next thing you need to understand before actually coding in OpenGL is some of the fundamental math underlying graphics programming. Don't worry, we'll start simple and ease into the more complex math so it won't hurt too badly.1 - Intermixing a functional library with an object-oriented language can sometimes lead to confusions. OpenGL ES has things it calls "objects", but they are not object as far as Objective-C is concerned. Usually, which type of object I'm referring to will be clear from the context, but when it's not, I'll try to identify whether “object” refers to an Objective-C object or an OpenGL object.
OpenGL ES 2.0 for iOS, Chapter 1 - Introduction
It is not an exaggeration to say that the iPhone SDK and the App Store have forever changed the way that mobile applications are developed and sold. By building the iPhone SDK on the foundation laid by NeXT with NextSTEP, which later became Apple's Cocoa framework for developing desktop applications, Apple was able to provide third-party developers of their new mobile platform with tools and some APIs that already had the benefit of over 20 years of use, testing, and documentation. Although iOS, of course, contains a great amount of new code designed specifically to handle the needs of a touch-based, mobile computing platform, many of the classes that implement fundamental behavior in the iOS SDK have been in regular use since the late 1980s; that code is extraordinarily robust and thoroughly documented.
But a mobile platformis different from a desktop or laptop computer in many ways, and not all of the technology that makes up the iPhone is as well-documented or as well-understood as the foundation classes inherited from NextSTEP. One such technology is OpenGL ES , a graphics library designed for use on smaller devices, with limited processing power and memory (the ES stands for embedded systems ). Although the iPhone, iPod touch, and iPad are, in many ways, engineering marvels, they are still considerably underpowered compared to today's laptop and desktop computers. They have less RAM, slower processors with fewer processing cores, and a less powerful GPU than even inexpensive general-purpose computers. iOS applications, such as games, that want to fully leverage the graphics capabilities of the iPhone generally have to use OpenGL ES to get the best possible performance out of the hardware.
Yet if you go looking for specific beginner-level information about how to use OpenGL ES on the iPhone, it can be hard to find. Although there are a great many books, tutorials, and articles on OpenGL, of which OpenGL ES is a subset, nearly every one starts out teaching something calleddirect mode , which doesn't exist in OpenGL ES (or the most recent OpenGL specification, for that matter). Direct mode was one of the earliest ways to interact with OpenGL, but it's not used much in practice because it's slow. In direct mode, you perform a separate C function call for every single piece of data or instruction you need to pass in to OpenGL. To draw a triangle, for example, you have to make four function calls (in addition to any setup code), one call to define the location of each of the three points that make up the triangle, then another function call to actually draw the triangle. For complex objects, direct mode code quickly becomes tedious and inefficient.
Direct mode was kept in workstation OpenGL for many years past when it was a viable option not just for backward compatibility, but also because it was a tremendous tool for learning. By having to break the drawing process down into all these individual function calls, the programmer who is new to graphics programming and the mathematics of drawing is able to conceptualize what is going on more easily. After spending a while with direct mode, new developers can begin to understand how OpenGL works; by the time they are introduced to more efficient ways of submitting data to OpenGL, they have a good grounding and are ready for the conceptually harder techniques.
Without direct mode, programmers new to OpenGL ES are forced to begin using these harder techniques immediately. There's no gradual entry into the OpenGL ES pool: you have to just jump right into the deep end. And if you don't already know how to swim, jumping in to the deep end can be pretty intimidating.
To make matters worse, to fully leverage the power of today's iOS devices, you have to use OpenGL ES 2.0, and OpenGL ES 2.0 has an even steeper learning curve than earlier versions. OpenGL ES 2.0 dropped support for something calledfixed pipeline rendering which provided a number of stock function calls for handling common tasks such as setting up lights, moving and rotating objects, and defining the part of the world to be rendered. Under the fixed pipeline, for example, if you wanted to rotate an object, you would simply call the built-in function glRotatef() before drawing, which would tell OpenGL ES how far and on what axis to rotate the object before drawing it. With OpenGL ES's focus on performance, once the programmable pipeline was introduced in OpenGL ES 2.0, support for the fixed pipeline was completely dropped, meaning all those convenient methods for setting up and moving objects around your scene are gone. OpenGL ES 1.1 applications will not even compile under OpenGL ES 2.0. Not only is OpenGL ES 2.0 the deep end of the pool, it's the deep end of a very deep, very wide, and very cold pool.
One of the difficulties in writing a book on introductory level OpenGL ES is choosing what to cover. The topic is expansive. The official OpenGL books alone amount to several thousand pages of material, and those generally assume a certain level of existing math and graphics programming knowledge. There's simply no way to cover the topic exhaustively in a single book. One of my personal frustrations when originally learning graphics programming was the assumption most books seemed to have that you already had a really strong math foundation and that information was still fresh in your mind. I'm not going to make that assumption. I don't expect you to have received a doctoral degree in mathematics before reading this book and writing your first OpenGL ES application. However, because graphics programming is so heavily dependent on math, you do need a basic working knowledge of high-school level math, especially basic geometry and trigonometry.
What I won't be doing is using C++.
I know that many OpenGL ES books and other resources use C++, and even operate under the assumption that any other language choice would be foolish. For iOS programming, that's simply an incorrect assumption.
Objective-C is the lingua franca of iPhone development. The entire Cocoa Touch framework is written in Objective-C, as are the foundation objects you'll need to pass to most of the iOS APIs. It is true that Objective-C and C++ code can work together using something called Objective-C++, and Objective-C++ is an amazing piece of engineering. But it has also been described as an “unholy marriage” and a “marriage of convenience” by engineers on Apple's compiler team. It's a great resource if you have large existing libraries of C++ code or if you're porting something that was written in C++ from another platform. But if you're starting from scratch on the iPhone, Objective-C really is the way to go.
The reason that Objective-C++ is an “unholy marriage” is because the two languages evolved from very different sources and use very different object models. C++ uses an object model derived from a programming language calledSimula . Simula-derived languages like C++ are strongly typed and use static dispatching, which means that determining how a member function gets called happens at compile time. Basically, C++ does a lot of checks and rules enforcement at compile time, restricting what you can do in order to prevent you from shooting yourself in the foot. Objective-C, on the other hand, uses an object model based on Smalltalk, which is loosely typed and dynamically dispatched. Objective-C is much more permissive, and defers many tasks to runtime that C++ handles at compile time. There are arguments for both approaches---as well as times when one is clearly a better choice---but any way you look at it, they are fundamentally different languages, far more than just the syntactical differences. As a result, you tend to use drastically different patterns when using the two languages.
The reasons most often given for using C++ are performance and portability. When it comes to performance, it is true that C++ has slightly less overhead when it comes to object creation and destruction compared to Objective-C's allocation and deallocation, as well as a little less overhead when it comes to calling member functions when compared with Objective-C's dynamic dispatch mechanism. However, in both cases, the overhead is more than using the low-level C functionality that both languages rest on top of. For example,free() malloc() is less costly than either C++'s new or Objective-C's alloc and init. When performance is potentially an issue (and performance is often a potential issue when doing graphics programming on an embedded device), I'll avoid the overhead of the object model completely and use straight C. Since both Objective-C and C++ are supersets of C, C code can be used in both C++ and Objective-C without any bridging or unholiness at all. As for portability, it is true that C++ is still a more commonly used language than Objective-C, though how much of an issue that is in the mobile space, where Java is the next most commonly used language after Objective-C, is debatable.
But a mobile platform
Yet if you go looking for specific beginner-level information about how to use OpenGL ES on the iPhone, it can be hard to find. Although there are a great many books, tutorials, and articles on OpenGL, of which OpenGL ES is a subset, nearly every one starts out teaching something called
Direct mode was kept in workstation OpenGL for many years past when it was a viable option not just for backward compatibility, but also because it was a tremendous tool for learning. By having to break the drawing process down into all these individual function calls, the programmer who is new to graphics programming and the mathematics of drawing is able to conceptualize what is going on more easily. After spending a while with direct mode, new developers can begin to understand how OpenGL works; by the time they are introduced to more efficient ways of submitting data to OpenGL, they have a good grounding and are ready for the conceptually harder techniques.
Without direct mode, programmers new to OpenGL ES are forced to begin using these harder techniques immediately. There's no gradual entry into the OpenGL ES pool: you have to just jump right into the deep end. And if you don't already know how to swim, jumping in to the deep end can be pretty intimidating.
To make matters worse, to fully leverage the power of today's iOS devices, you have to use OpenGL ES 2.0, and OpenGL ES 2.0 has an even steeper learning curve than earlier versions. OpenGL ES 2.0 dropped support for something called
Don't worry if you don't understand what the pipeline is, or what the difference between a fixed and a programmable pipeline is. That will be explained in future chapters.Think of this book as a life vest for OpenGL ES 2.0. You're still going to have to jump into the deep end right from the start, but I should be able to keep your head above water most of the time.
What You Need to Know
To use this book, you don't need to already know anything about OpenGL, OpenGL ES, or even about graphics programming in general. You will, however, need to understand the basics of programming and, specifically, programming in Objective-C for iOS devices. This means you'll need to be comfortable with both the Objective-C language, as well as straight C. You should have some familiarity with the various frameworks that make up the iPhone SDK and be familiar with basic programming concepts, including memory management. Although I'll be going slowly as I introduce you to 3D concepts, I won't be explaining basic programming concepts such as the difference between allocating memory on the stack and on the heap. If you're rusty or unsure, it's a good idea to brush up on programming basics before proceeding. You also should be familiar with the basics of working in Xcode.One of the difficulties in writing a book on introductory level OpenGL ES is choosing what to cover. The topic is expansive. The official OpenGL books alone amount to several thousand pages of material, and those generally assume a certain level of existing math and graphics programming knowledge. There's simply no way to cover the topic exhaustively in a single book. One of my personal frustrations when originally learning graphics programming was the assumption most books seemed to have that you already had a really strong math foundation and that information was still fresh in your mind. I'm not going to make that assumption. I don't expect you to have received a doctoral degree in mathematics before reading this book and writing your first OpenGL ES application. However, because graphics programming is so heavily dependent on math, you do need a basic working knowledge of high-school level math, especially basic geometry and trigonometry.
What You Need to Have
In order to get the most out of this book, you need access to an Intel Mac and be a member of Apple's iPhone Developer Program. Make sure to download the latest version of the iPhone SDK before beginning. Although you'll be able to run much of the code in this book on the iPhone Simulator, to get the most out of it, you'll need to be able to run applications on your iPhone, iPad, or iPod touch, so one of the paid iPhone SDK memberships, which give you the ability to run applications on a physical device, is highly recommended. OpenGL ES programming can be very processor-intensive, and the iPhone Simulator running on your Mac won't give you a good indication of how well your programs will perform on an actual iOS device, because all iOS devices have a slower processor and less RAM than even the lowest-end Macs.A Note About Language Choice
Before we get started, I want to take a quick second to talk about my choice of programming languages. In this book, I'm going to be using Objective-C. Objective-C is a superset of C, and in many places, I will leverage that fact and use good old-fashioned C functions, structs, and datatypes instead of using higher-level Objective-C objects.What I won't be doing is using C++.
I know that many OpenGL ES books and other resources use C++, and even operate under the assumption that any other language choice would be foolish. For iOS programming, that's simply an incorrect assumption.
Objective-C is the lingua franca of iPhone development. The entire Cocoa Touch framework is written in Objective-C, as are the foundation objects you'll need to pass to most of the iOS APIs. It is true that Objective-C and C++ code can work together using something called Objective-C++, and Objective-C++ is an amazing piece of engineering. But it has also been described as an “unholy marriage” and a “marriage of convenience” by engineers on Apple's compiler team. It's a great resource if you have large existing libraries of C++ code or if you're porting something that was written in C++ from another platform. But if you're starting from scratch on the iPhone, Objective-C really is the way to go.
The reason that Objective-C++ is an “unholy marriage” is because the two languages evolved from very different sources and use very different object models. C++ uses an object model derived from a programming language called
The reasons most often given for using C++ are performance and portability. When it comes to performance, it is true that C++ has slightly less overhead when it comes to object creation and destruction compared to Objective-C's allocation and deallocation, as well as a little less overhead when it comes to calling member functions when compared with Objective-C's dynamic dispatch mechanism. However, in both cases, the overhead is more than using the low-level C functionality that both languages rest on top of. For example,
Let's Go!
We've got a lot to do, and a lot of it is really cool. I'll try and get Chapter 2 posted quickly.Lifting the Skirt
MartianCraft has received a surge of requests for quotes and proposals in the several weeks. A disturbing trend that I've been noticing in some of these proposals is that more and more of the people who contact us are wanting us to sign NDAs before they'll lift their skirts even a little. Often, we can't get the most basic information about a project, not even things like ballpark budget, timeline, or type of application until we've signed an NDA, often a pro-forma NDA that was downloaded from the web.
The last thing any reputable iOS dev shop is interested in doing is stealing your idea. First of all, it would destroy our business if we did that. NDA or not, it would be unethical. This is what we do for a living. If we were to steal an idea and publish it as our own, word would get out and people wouldn't trust us. Our business would die even without ever being sued.
More than that, though: Ideas, with only rare exceptions, have little value without the ability to execute on the idea and execute on it well. I guarantee you that no matter how great you think your idea is, we have several of our own that we'd rather be spending our time on. But we don't even have time to work on our own cool side projects right now, never mind steal yours.
It's absolutely understandable, of course, to reserve certain strategically important details until after a contract is signed, but you have to give us enough information for us to decide whether we're a good fit for your project.
Every NDA or contract we sign costs us money, and not an inconsiderable amount of money. Every single one goes to our lawyer before we'll sign it, and most of them have to be modified and negotiated. It's a costly process. Even the simplest NDAs cost MartianCraft hundreds of dollars by the time we've signed it. We're not going to spend that if we don't have some notion that it's a good project for us and that we have the resources to do it well. We'd quite honestly go bankrupt if we were to forward every NDA request we got to our attorney.
If we know a little about your timeline and budget and a brief synopsis of the app you want to build, we're far more likely to submit a proposal. If you're not willing to give us even the most basic information, then we're going to politely decline your NDA and pass on the project unless you're a Fortune 500 company… maybe.
Here's the important thing for you to realize if you're looking for any mobile developer, but especially an iOS developer: there are nowhere near enough competent, experienced mobile developers right now to meet the demand. By now, all the large companies have realized that mobile is the strategic battleground for the next several years. As a result, experienced mobile developers rarely have to look for work. MartianCraft has existed for less than a year. In that time, the only advertising we've done is to put a banner ad here on my blog, and yet we already have had to turn down at least as much work as we've accepted. I say that not to brag, but to show what the current state of the market is. It's not unusual for us to receive a half-dozen requests for proposals in a single day when you combine requests to MartianCraft and those that come to us individually. When we don't submit a bid on one of those proposals, it's not out of hubris, but rather out of practical necessity.
We are far from alone in this. All of us have friends in other longer-established mobile dev shops, and it's the same story all around. There's a lot of work — a lot of interesting work — and simply no way to accept every interesting project that comes along.
If you insist on an NDA before you give any information at all, you are potentially limiting your pool to the developers who are desperate for work, and given just how much mobile dev work there is out there right now, I'm really not sure that you want to limit your talent pool to just the ones who are desperate for work.
The last thing any reputable iOS dev shop is interested in doing is stealing your idea. First of all, it would destroy our business if we did that. NDA or not, it would be unethical. This is what we do for a living. If we were to steal an idea and publish it as our own, word would get out and people wouldn't trust us. Our business would die even without ever being sued.
More than that, though: Ideas, with only rare exceptions, have little value without the ability to execute on the idea and execute on it well. I guarantee you that no matter how great you think your idea is, we have several of our own that we'd rather be spending our time on. But we don't even have time to work on our own cool side projects right now, never mind steal yours.
It's absolutely understandable, of course, to reserve certain strategically important details until after a contract is signed, but you have to give us enough information for us to decide whether we're a good fit for your project.
Every NDA or contract we sign costs us money, and not an inconsiderable amount of money. Every single one goes to our lawyer before we'll sign it, and most of them have to be modified and negotiated. It's a costly process. Even the simplest NDAs cost MartianCraft hundreds of dollars by the time we've signed it. We're not going to spend that if we don't have some notion that it's a good project for us and that we have the resources to do it well. We'd quite honestly go bankrupt if we were to forward every NDA request we got to our attorney.
If we know a little about your timeline and budget and a brief synopsis of the app you want to build, we're far more likely to submit a proposal. If you're not willing to give us even the most basic information, then we're going to politely decline your NDA and pass on the project unless you're a Fortune 500 company… maybe.
Here's the important thing for you to realize if you're looking for any mobile developer, but especially an iOS developer: there are nowhere near enough competent, experienced mobile developers right now to meet the demand. By now, all the large companies have realized that mobile is the strategic battleground for the next several years. As a result, experienced mobile developers rarely have to look for work. MartianCraft has existed for less than a year. In that time, the only advertising we've done is to put a banner ad here on my blog, and yet we already have had to turn down at least as much work as we've accepted. I say that not to brag, but to show what the current state of the market is. It's not unusual for us to receive a half-dozen requests for proposals in a single day when you combine requests to MartianCraft and those that come to us individually. When we don't submit a bid on one of those proposals, it's not out of hubris, but rather out of practical necessity.
We are far from alone in this. All of us have friends in other longer-established mobile dev shops, and it's the same story all around. There's a lot of work — a lot of interesting work — and simply no way to accept every interesting project that comes along.
If you insist on an NDA before you give any information at all, you are potentially limiting your pool to the developers who are desperate for work, and given just how much mobile dev work there is out there right now, I'm really not sure that you want to limit your talent pool to just the ones who are desperate for work.
Update on OpenGL ES 2.0
My editor at the Pragmatic Programmers has informed me that I will be able to post the chapters of my OpenGL ES blog once the cancellation is complete. I have nothing but great things to say about my experience with the folks there. Good people all around. If you get a chance to write for them, you'd be foolish to pass up the opportunity.
So, once my cancellation letter arrives, I will begin prepping chapters for posting. I still don't have much in the way of free, so I wouldn't expect more than a chapter a week. I have to scrub the content both for copy edits and for potential NDA violations and then convert from DocBook to HTML.
So, once my cancellation letter arrives, I will begin prepping chapters for posting. I still don't have much in the way of free, so I wouldn't expect more than a chapter a week. I have to scrub the content both for copy edits and for potential NDA violations and then convert from DocBook to HTML.
iOS Secret Meeting
There have been reports lately of Apple holding a secret conference for iOS developers. Now, let me just state up front so there's no misunderstanding: Other than the normal news outlets, I haven't heard any information about such a conference - I'm certainly not invited if there is such a thing going on. This post is just conjecture on my part.
But I'm not sure why this is news. Apple constantly has strategically important developers (and other partners, like wireless carriers) out to Cupertino to work on future product announcements and to be informed about future products. It certainly shouldn't be news to anyone that the people who get up on stage with Steve at keynotes and presentations (plus everybody involved behind the scenes) knew ahead of time that they would be doing so.
If you follow a lot of iOS developers, you'll pick up subtle hints about when some of them are on campus or on their way there. It might just be a "Wheels down SFO" tweet, a comment about the food at Caffe Macs (the cafeteria at 1 Infinite Loop which is quite excellent), or a dinner with certain Apple employees, but the signs are there if you know what to look for.
Unsurprisingly, Apple is just as careful about keynotes as it is with everything else. As a result there are constant "summits" going on in the weeks before any public announcement. Since Apple now spreads their product announcements around the calendar year, that means it's an almost constant ebb and flow of strategic partners.
The process to be involved with a keynote presentation is long, stressful, and involves many trips to Cupertino. I can't say anything more specific about the process without betraying confidences (I've never been directly involved myself), but rest assured that despite Apple's famous secrecy, if you're at all involved with the developer community, then there are likely people outside Apple whom you've socialized with who knew a fair bit about certain products before they were released. Even people who aren't directly involved with a keynote presentation have to, at times, find out information about products early, and in some cases even get access to pre-release hardware (though usually with strong precautions talem to keep photos or other info from leaking).
If this is a surprise to you, chalk that up to the fact that the third party developers who are involved understand and respect Apple's desire for secrecy and want to continue being involved with the process. Apple is not known for being forgiving to those who leak information of that nature.
So, is there something even larger than normal going on next week, perhaps a replacement for the Tech Talk World Tours of past years? I don't know. It's absolutely possible. But, what seems more likely to me is that Business Insider simply got a whiff of information about an ongoing process and interpreted it incorrectly. Apple is never idle, and we're less than a month away from 4.2 being publicly released. It's altogether possible (I'd say likely) that there will be hardware or other software announcements that will coincide with release of 4.2.
Frankly, I'd find it far more surprising if there wasn't a flurry of third-party developers going in and out of Cupertino right now and for the next few weeks. Whether it's a formal summit of any size, I don't know, but I have my doubts. The more people involved with something like that, the harder it is to keep it secret and the more likely a leak is. Right now everything I can find online leads back to the original Business Insider story. Despite requests for anonymous information, no new information seems to have come out.
My bets are on business-as-usual pre-announcement activity, not some secret conference. If it is a secret conference, the participants are likely only the most strategically important partners: people who have been involved with pre-release products previously.
But I'm not sure why this is news. Apple constantly has strategically important developers (and other partners, like wireless carriers) out to Cupertino to work on future product announcements and to be informed about future products. It certainly shouldn't be news to anyone that the people who get up on stage with Steve at keynotes and presentations (plus everybody involved behind the scenes) knew ahead of time that they would be doing so.
If you follow a lot of iOS developers, you'll pick up subtle hints about when some of them are on campus or on their way there. It might just be a "Wheels down SFO" tweet, a comment about the food at Caffe Macs (the cafeteria at 1 Infinite Loop which is quite excellent), or a dinner with certain Apple employees, but the signs are there if you know what to look for.
Unsurprisingly, Apple is just as careful about keynotes as it is with everything else. As a result there are constant "summits" going on in the weeks before any public announcement. Since Apple now spreads their product announcements around the calendar year, that means it's an almost constant ebb and flow of strategic partners.
The process to be involved with a keynote presentation is long, stressful, and involves many trips to Cupertino. I can't say anything more specific about the process without betraying confidences (I've never been directly involved myself), but rest assured that despite Apple's famous secrecy, if you're at all involved with the developer community, then there are likely people outside Apple whom you've socialized with who knew a fair bit about certain products before they were released. Even people who aren't directly involved with a keynote presentation have to, at times, find out information about products early, and in some cases even get access to pre-release hardware (though usually with strong precautions talem to keep photos or other info from leaking).
If this is a surprise to you, chalk that up to the fact that the third party developers who are involved understand and respect Apple's desire for secrecy and want to continue being involved with the process. Apple is not known for being forgiving to those who leak information of that nature.
So, is there something even larger than normal going on next week, perhaps a replacement for the Tech Talk World Tours of past years? I don't know. It's absolutely possible. But, what seems more likely to me is that Business Insider simply got a whiff of information about an ongoing process and interpreted it incorrectly. Apple is never idle, and we're less than a month away from 4.2 being publicly released. It's altogether possible (I'd say likely) that there will be hardware or other software announcements that will coincide with release of 4.2.
Frankly, I'd find it far more surprising if there wasn't a flurry of third-party developers going in and out of Cupertino right now and for the next few weeks. Whether it's a formal summit of any size, I don't know, but I have my doubts. The more people involved with something like that, the harder it is to keep it secret and the more likely a leak is. Right now everything I can find online leads back to the original Business Insider story. Despite requests for anonymous information, no new information seems to have come out.
My bets are on business-as-usual pre-announcement activity, not some secret conference. If it is a secret conference, the participants are likely only the most strategically important partners: people who have been involved with pre-release products previously.
OpenGL ES 2.0 Book
I've been getting a lot of questions lately about the status of my OpenGL ES 2.0 book for PragProg. What I've been telling people is: "it's about half done but I have no idea when I'll be able to finish it". To say I've been busy lately would be an understatement of epic proportions. As a part-owner of a business in its first year, being too busy is a great problem to have, but it does take its tolls in both subtle and not-so-subtle ways.
When you combine how busy I am with the fact that I've been completely unable to get even ballpark information about when Xcode 4 will go GM (the book is heavily based on Xcode 4), it means I simply cannot nail down a production schedule for the book. Even if I had time to finish the book right now, it can't be published until the Xcode 4 NDA drops. It also makes no sense to revise the book to a version of Xcode which is soon to become obsolete.
As a result, today, I made the difficult decision, along with my editor at Prags, to indefinitely shelve the OpenGL ES 2.0 book project. I would have liked to keep the project open and work on it whenever I have time, but that wouldn't have been fair to my publisher. They have to plan their production pipeline very carefully and a book with no set timeline throws a real monkey wrench into that process, which I really don't want to do. The door has been left open for me pick the book up in the future if and when I have time, but for now, it's coming off the production schedule to free up resources for other authors' books.
I have requested permission to post the existing seven chapters of the manuscript to my blog (tweaked so I'm not violating the Xcode 4 NDA, of course). From a contractual and legal point of view, I cannot just post what I've written without the the permission of my publisher. Prags has been nothing but fair, patient, and a pleasure to deal with and I want to make sure I'm just as fair to them and also comply fully with my contract.
However, if I can find a path to posting the chapters that's legal, ethical, and doesn't harm my relationship with Prags, I will do so.
When you combine how busy I am with the fact that I've been completely unable to get even ballpark information about when Xcode 4 will go GM (the book is heavily based on Xcode 4), it means I simply cannot nail down a production schedule for the book. Even if I had time to finish the book right now, it can't be published until the Xcode 4 NDA drops. It also makes no sense to revise the book to a version of Xcode which is soon to become obsolete.
As a result, today, I made the difficult decision, along with my editor at Prags, to indefinitely shelve the OpenGL ES 2.0 book project. I would have liked to keep the project open and work on it whenever I have time, but that wouldn't have been fair to my publisher. They have to plan their production pipeline very carefully and a book with no set timeline throws a real monkey wrench into that process, which I really don't want to do. The door has been left open for me pick the book up in the future if and when I have time, but for now, it's coming off the production schedule to free up resources for other authors' books.
I have requested permission to post the existing seven chapters of the manuscript to my blog (tweaked so I'm not violating the Xcode 4 NDA, of course). From a contractual and legal point of view, I cannot just post what I've written without the the permission of my publisher. Prags has been nothing but fair, patient, and a pleasure to deal with and I want to make sure I'm just as fair to them and also comply fully with my contract.
However, if I can find a path to posting the chapters that's legal, ethical, and doesn't harm my relationship with Prags, I will do so.
Tectonic+ 1.0 for iPhone and iPad with 3D support
The new version of this unique app will provide Apple consumers with 3D support.
Now Recent earthquakes, hurricanes and tornadoes are displayed on a 3D interactive globe and the users are able to move a 3D glove with their fingers to any direction.
You can zoom in and out of a particular area of the globe by pinch on the globe with your fingers. Spread your two fingers apart or squeeze them together by this actions you will zoom in and zoom out.
Tectonic+ 1 will help you to experience and explore a lot of new and interesting things.
Main Features:
* Recent earthquakes displayed on a 3D interactive globe
* Filter options by Magnitude, Quantity and Timeframe
* Displays current Hurricanes and Tordanoes
* Displays the most active volcanoes on the planet
* Displays the main Tectonic+boundaries
* Displays current Weather for the main cities of the world
* Displays your actual location on the globe
* Three different earth appearance with many options
* Full Google Map integration to display more details
* iPhone 3GS, 4, iPod touch (3rd Gen), iPod touch (4th Gen), and iPad
* Requires iOS 3.1.3 or later
* 15.8 MB
Pricing and Availability:
When you purchase the iPhone version, the iPad version is free and vice versa. All updates are free for lifetime. Tectonic+ is available for $0.99 (USD) only until end of December 2010. It's a special introductory price.
For more information click here
Wednesday, October 27, 2010
Nightstand - An innovative iOS Clock with Alarm/Weather/Radio/Browser
The Professional Alarm Clock gives you ability to check the weather, wake to music and read the morning news. All in one application. With Nightstand you will find several common tasks simplified, as alarm setting, in order to ensure easy, intuitive, correct functioning.
Animations and a designer UI round out the experience for users, providing a custom-crafted environment intended to be "the ultimate app for your sleep/wake routine".
Some features:
* Wake to alarm or music
* "Sleep timer" turns off music as you drift off to sleep
* "Backup alarm" ensures you wake up
* Internet radio and iTunes integration
* Music visualizer
* Local weather and weather graphics
* Infinite tabs in browser
* Simplified "quick-dial" favorites
* Full suite of standard features including snooze, audio controls, and web navigation controls
* iPhone, iPod touch, and iPad
* Requires iOS 3.1.3 or later
* 17.2 MB
Pricing and Availability:
Nightstand - The Professional Alarm Clock 1.0 is $1.99 USD and available worldwide exclusively through the App Store in the Lifestyle category.
For more information click here
Tuesday, October 26, 2010
Casino for iPad - New Must-Have App for Casino Lovers
These 10 games are: American and European roulette, Burning Cherry and Red Dragon Tale slot machines, Casino Hold'em and Poker Three, Blackjack Switch and Blackjack Surrender, Deuces Wild and Jacks or Better video poker.
The games are designed professionally and make a chic of real casino with casino-style music in the background and a user-friendly interface. Casino for iPad contains a bank where players can buy chips and cash their wins. The players only use game money to get chips and make bets extra payments are not required.
For the competition-hungry players Casino offers additional feature the availability of Leader Board of the OpenFeint platform. Players can submit their their highest scores, challenge other casino fans and successful players can show off their records on Facebook and Twitter.
Compatible with iPad, iPhone and iPod touch, this is the ultimate collection of user-favorite casino games with more waiting to be added in updates.
* iPhone, iPod touch, and iPad
* Requires iOS 3.2 or later
* 92.5 MB
Pricing and Availability:
Casino for iPad 1.0 is $5.99 USD and available worldwide exclusively through the App Store in the Games category.
For more information click here
Subscribe to:
Posts (Atom)
